Um fio de aço suspenso verticalmente, conforme ilustrado na figura, tem uma área A de seção transversal e um comprimento inicial . Uma força F para baixo, aplicada à extremidade do fio faz com que este se estique. A tensão normal no fio varia linearmente de acordo com , em que é a deformação, dada por , em que x é o comprimento do fio esticado. C é uma constante do material (módulo de Young). Admitindo que a área da seção transversal permanece constante, (a) obtenha uma expressão para o trabalho realizado sobre o fio, (b) calcule o trabalho realizado sobre o fio, em ft.lbf, e a magnitude da força dirigida para baixo, em lbf, se 10 ft (3,0 m), x =10,01 ft (3,0 m), A = 0,1 in² ( m²), e C = lbf/in² ( Pa).
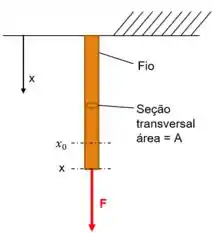
Passo 1
Temos muita informação no texto, bem confuso!
Vamos dar uma organizada nos dados:
Bem melhor de observar cada coisa assim né?
Já podemos organizar:
Beleza?
Passo 2
Agora vamos achar essa expressão para o trabalho na letra (a). Temos que o trabalho de tração pode ser expresso como:
Já temos que:
e
Então substituindo na fórmula do trabalho:
Como C, A e são constantes, podemos colocar para fora da integral!
Passo 3
Para achar o trabalho na letra (b) é só substituir na equação achada anteriormente!
Já para achar a força, temos:
Lembra que ?