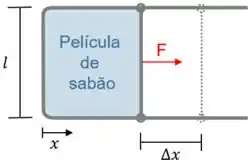
Uma película de sabão é suspensa em uma armação de arame, confirme a figura. O arame corrediço é deslocado por meio de uma força aplicada F. Considerando que a tensão superficial permanece constante, (a) obtenha uma expressão para o trabalho realizado ao esticar a película, em termos da tensão superficial , do comprimento e do deslocamento , (b) determine o trabalho realizado, em J, se, , = 0,5 cm e .
Passo 1
Primeiro vamos lembrar que desse caso vamos ter 2 áreas superficiais na película! Isso mesmo, a área da frente que tá sendo vista por nós na figura e a área de trás!
Então temos que a área superficial total da película é:
Derivando essa equação no tempo:
A questão nos deu também alguns dados:
Vamos para os cálculos!
Passo 2
Agora vamos achar essa expressão para o trabalho da letra (a). Temos que o trabalho relativo a um aumento de área superficial se dá por:
Já temos que:
Então substituindo na fórmula do trabalho:
Como e são constantes, podemos colocar para fora da integral!
Passo 3
Para achar o trabalho na letra (b) agora é só substituir os dados na equação achada anteriormente!