A forca gerada por uma mola e dada por , ondee a constante da mola e e a deformação da mola. A mola da figura tem uma constante de mola de . As pressões são , e . Se os diâmetros dos pistões correspondem a e, quanto à mola se deformara?
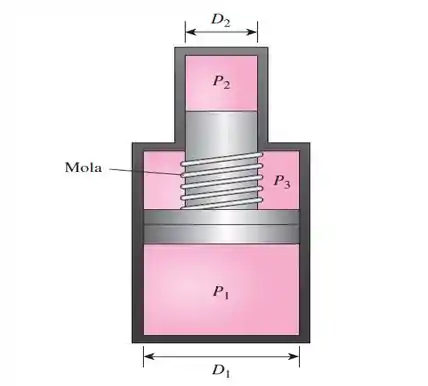
Passo 1
Utilizaremos a fórmula de pressão:
E a lei de Hooke que já foi enunciada do enunciado:
Certo, vamos executar um diagrama de forças aqui:
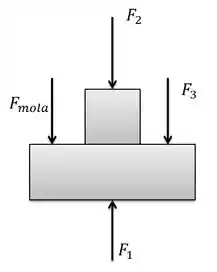
Certo com isto podemos fazer um somatório de forças, em que substituiremos as forças pelo produto das pressões e áreas.
Passo 2
Substituindo pelo produto das pressões e áreas e abrindo :
Substituindo as áreas por, :
Chamar um pouquinho de atenção para , será encontrado pela subtração dos diâmetros de e .
Isolando e substituindo os valores temos: