Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 53
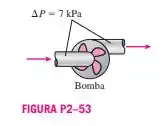
A força motriz para o escoamento de fluidos é a diferença de pressão, e uma bomba opera elevando a pressão de um fluido (convertendo o trabalho mecânico de eixo em energia de escoamento). O consumo de energia elétrica de uma bomba de gasolina em operação é de 3,8 kW. Considerando que a diferença de pressão entre a saída e a entrada da bomba é de 7 kPa e as variações da velocidade e altura são desprezíveis, determine a máxima vazão volumétrica possível de gasolina.
Passo 1
Ao fazer o balanço de energia, temos que a energia na entrada e na saída da bomba são iguais, isto porque a bomba opera num regime permanente, ou seja, em qualquer momento que observarmos a bomba ela estará operando da mesma forma que em qualquer outro momento. Assim:
Temos que a bomba precisa de 3,8 kW para operar, ou seja, 3,8 kW “entram” para que a bomba funcione. Assim,
Passo 2
Rearranjando a expressão, temos:
Temos que, a taxa mássica pode ser dada por , assim, a equação fica da seguinte forma:
Passo 3
Queremos saber a vazão volumétrica da gasolina, então vamos isolar o termo da expressão e vamos substituir os dados fornecidos pelo enunciado, logo
Temos que 1 kJ equivale a 1 kPa, logo, nosso resultado é equivalente a 0,543 .
Resposta
A máxima vazão volumétrica possível da gasolina é de 0,543 .