Um gás está contido em um cilindro provido de um êmbolo de área . Como na Fig. 1.8 (a). A relação entre a pressão e o volume do gás a uma temperatura constante é mostrada na Fig. 1.8 (b). Em uma figura semelhante, esboce gráficos da razão da força externa para a área , , como uma função de , sendo o gás

b) Expandido lentamente à temperatura .

Há uma força de atrito de deslizamento entre o êmbolo e o cilindro.

Temos que para que o sistema esteja expandindo, é necessário que

Ou seja, temos dividindo os dois lados da inequação por , que:

. Ou seja, como sabemos a relação de com , é obtida através da subtração de uma constante no gráfico. Temos então:

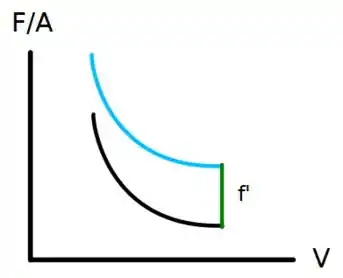
A linha azul está representando a Fig 1.8 (b). A nossa razão deve ser aproximadamente representada pela curva preta, necessariamente precisamos de valores levemente menores para termos a expansão.

A questão foi isso, te vejo na próxima! Tchauzinho!