Um gás contido em um conjunto cilindro-pistão passa por três processos em série:Processo 1-2: volume constante de p 1 = 1 bar, V 1 = 4m³ até o estado 2, em que p 2 = 2 bar.Processo 2-3: compressão até V 3 = 2 m³, durante a qual a relação pressão-volume é p . V = c o n s t a n t e . Processo 3-4: pressão constante até o estado 4, em que V 4 = 1m³.Esboce os processos em série em um diagrama p-V e determine o trabalho para cada processor, em kJ.

Enunciado

Vamos lá! Como o enunciado nos deu tudo passo-a-passo, vamos fazer assim também.

Primeiro vamos para o processo 1-2.

Como é um processo a volume constante, então, . Assim temos os seguintes dados para o processo:

Vamos fazer um esboço desse processo no diagrama p-V?

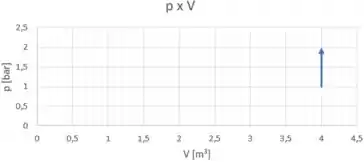
Opa! O gráfico é uma reta vertical, certo? Não tem área sob a curva. Isso quer dizer que nosso trabalho é zero!

Agora vamos fazer a mesma análise para o processo 2-3!

O enunciado nos fala que o volume no estado 3 é 2 m³. Mas continuamos sem ter a pressão do estado 3, como podemos acha-la?

Segundo o enunciado o processo 2-3 segue a relação ! Isso quer dizer que:

Agora temos todos os dados do processo 2-3:

Vamos adicionar o gráfico desse novo processo naquele antigo?

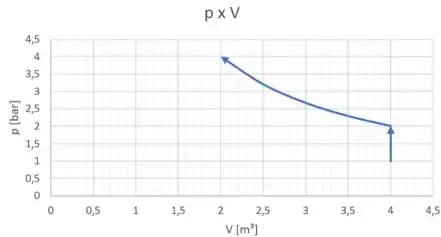
Meio difícil calcular o trabalho pela área do gráfico nesse caso né? Vamos então utilizar a formula do trabalho:

No processo temos que

Ao mesmo temo que

Então voltando para o trabalho:

Passando para kJ:

Por fim, temos o processo 3-4, o qual acontece em pressão constante. Então, e o volume do estado 4 é 1 m³. Com isso temos os dados do processo:

Adicionando o gráfico desse processo vamos ter o gráfico completo de todo o processo 1-4!

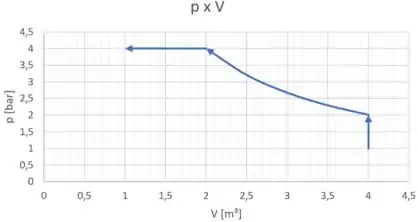
O cálculo do trabalho do processo 3-4 pode ser feito através da área sob a região nova no gráfico:

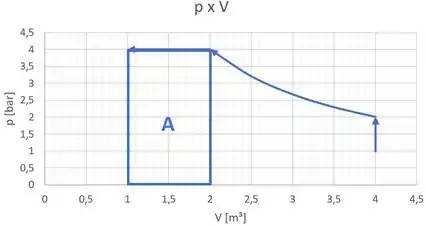
Como é um processo de compressão, o trabalho será o negativo da área!!!

Passando para kJ temos:

Processo 1-2: W = 0 kJProcesso 2-3: W = -554,5 kJProcesso 3-4: W = -400 kJ