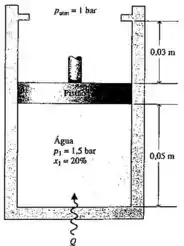
Como ilustrado na Fig. P3.71, água contida em um conjunto cilindro-pistão, inicialmente a 1,5 bar e 20% de título é aquecida a pressão constante até que o pistão atinge os esbarros. A transferência de calor continua até que a água atinja o estado de vapor saturado. Apresente os processos em série da água em um esboço do diagrama T–υ. Para o processo global relativo à água, determine o trabalho e o calor transferido, ambos em kJ/kg. Os efeitos das energias cinética e potencial não são significativos.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica! Nosso bom e lindo sistema pistão cilindro está de volta, sei que você deve estar tendo sonhos com ele e ele sempre volta 😊

Passo 2
O sistema pistão cilindro é mostrado abaixo
Desenhando o diagrama
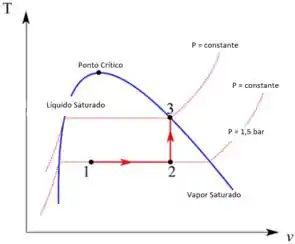
Passo 3
Esse pistão vai se mover com pressão constante até que ele encoste nos apoios, como a água é uma mistura a temperatura também permanece constante e devido à expansão o volume específico aumenta (não há mudança de massa então o volume específico muda com o volume).
Passo 4
Obtendo as propriedades do estado 1 da Tabela A-3 “Propriedades de Água Saturada (Líquido-Vapor) – Tabela de Pressão” a uma pressão saturada de
Calculando a energia interna específica no estado 1 usando a relação
Calculando o volume específico no estado 1 usando a relação
Passo 5
Calculando o volume do cilindro no estado 1 usando a relação
Calculando o comprimento do acesso no estado 2 usando a relação
Calculando o volume do cilindro no estado 2 usando a relação
Passo 6
Considerando a seguinte relação pro volume específico no estado 2
Considerando a seguinte relação pro volume específico no estado 1
Calculando a razão
Passo 7
Obtendo as propriedades no estado 2 da Tabela A-3 “Propriedades de Água Saturada (Líquido-Vapor) – Tabela de Pressão” para uma pressão
Calculando o título no estado 2
Passo 5
Calculando a energia interna específica no estado 2 usando a relação
O volume específico no estado 3 é igual ao do estado 2
Passo 6
Obtendo as propriedades no estado 3 da Tabela A-3 “Propriedades de Água Saturada (Líquido-Vapor) – Tabela de Pressão” em e
Calculando a pressão correspondente usando interpolação
Obtendo o valor de energia interna específica no estado 3 usando interpolação
Passo 7
Calculando o trabalho feito por unidade de massa no processo 1-2 usando a relação
Já que o processo 2-3 é com volume constante,
Calculando o trabalho total
Passo 8
Calculando a transferência de calor para o processo inteiro