Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 132
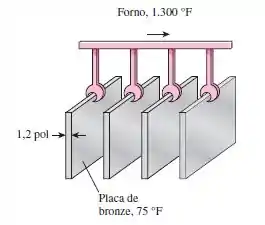
Em uma instalação, placas de latão quadradas de e com , inicialmente a uma temperatura uniforme de , são aquecidas quando passam por um forno a a uma taxa de por minuto. Considerando que as placas permanecem no forno até que a sua temperatura média suba para, determine a taxa de transferência de calor para as placas na fornalha e a taxa de destruição de energia associada com esse processo de transferência de calor.
Passo 1
Vamos lá! A questão nos afirma que grandes placas de latão são aquecidas em um forno a uma taxa de . A taxa de transferência de calor para as placas no forno e a taxa de destruição por esforço associada a este processo de transferência de calor devem ser determinadas.
Assumindo que:
- As propriedades térmicas das placas são constantes.
- As alterações na cinética e nas energias potenciais são insignificantes.
- A temperatura ambiente é de .
A densidade e o calor específico do latão são dados a ser
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que levamos a placa para ser o sistema. O balanço energético para este sistema fechado pode ser expresso como
A massa de cada placa e a quantidade de transferência de calor para cada placa é
Então a taxa total de transferência de calor para as placas torna-se
Passo 3
Tomamos novamente uma única placa como o sistema. A entropia gerada durante este processo pode ser determinada através da aplicação de um equilíbrio de entropia num sistema alargado que inclui a placa e o seu ambiente imediato, de modo a que a temperatura limite do sistema alargado esteja sempre a :
onde
Substituindo,
Então a taxa de geração de entropia torna-se
A energia destruída durante um processo pode ser determinada a partir de um balanço de energia ou diretamente a partir de sua definição ,