Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 129
O tanque de armazenamento de ar comprimido mostrado na Fig. P8–129 tem um volume de e contem inicialmente ar a e . Em um processo, o compressor isentrópico passa a comprimir ar, que entra no compressor a e até que o tanque esteja cheio, a e . Todas as trocas de calor são com o ar circundante a . Calcule a mudança no potencial de trabalho do ar armazenado no tanque. Como isso se compara com o trabalho necessário para comprimir o ar enquanto o tanque estava sendo preenchido?
Passo 1
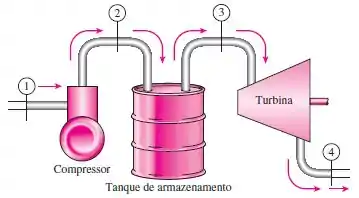
Vamos lá! A questão nos afirma que é considerado um sistema composto por um compressor, um tanque de armazenamento e uma turbina, como mostrado na figura. A mudança no esforço do ar no tanque e o trabalho necessário para comprimir o ar à medida que o tanque estava a ser enchido devem ser determinados.
Assumindo que:
- As mudanças na cinética e nas energias potenciais são insignificantes.
- O ar é um gás ideal, com aquecimento específico constante.
As propriedades do ar à temperatura ambiente são , c_p = 1.005 kJ/kg⋅K, c_v = 0.718 kJ/kg⋅K, k = 1.4 (Tabela A-2a).
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que a massa de ar inicial no tanque é
e a massa final no tanque é
Uma vez que o compressor funciona como um dispositivo isentrópico,
A conservação da massa aplicada ao tanque dá
enquanto a primeira lei dá
Passo 3
Empregando a equação ideal de gás de estado e usando constantes aquecedores específicos, expande este resultado para
Usando a relação de temperatura através do compressor e multiplicando por dt coloca este resultado na forma
Quando integrado, ele cede ( e significam estados iniciais e finais).
Passo 4
Note que, o resultado negativo mostra que o calor é transferido do tanque. A aplicação da primeira lei ao tanque e ao compressor dá
que se integra a
Após rearranjo,
Observe que, o sinal negativo mostra que o trabalho é feito no compressor. Quando a primeira e segunda leis combinadas são reduzidas para caber o sistema do compressor e do tanque e o balanço de massa incorporado, o resultado é
que, quando integrada ao longo do processo, se torna
Esta é a energia da mudança do ar armazenado no tanque.