Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 130
O ar armazenado no tanque do problema anterior e agora liberado pela turbina isentrópica até que o conteúdo do tanque esteja a e . A pressão e sempre na saída da turbina, e todas as trocas de calor são com o ar circundante que está a . Como o trabalho total produzido pela turbina se compara com a mudança no potencial de trabalho do ar no tanque de armazenamento?
Passo 1
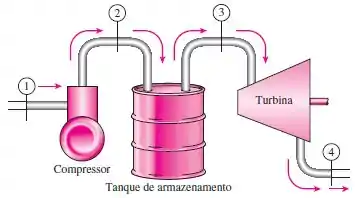
Vamos lá! A questão nos afirma que o ar armazenado no tanque do sistema mostrado na figura é liberado através da turbina isentrópica. O trabalho produzido e a mudança na exaustão do ar no tanque devem ser determinados.
Assumindo que:
- As mudanças na cinética e nas energias potenciais são insignificantes.
- O ar é um gás ideal, com aquecimento específico constante.
As propriedades do ar à temperatura ambiente (Tabela A-2a).
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que a massa de ar inicial no tanque é
e a massa final no tanque é
A conservação da massa é
enquanto a primeira lei dá
Passo 3
Empregando a equação ideal de gás de estado e usando constantes aquecedores específicos, expande este resultado para
Quando isto é integrado ao longo do processo, o resultado é (i e f significam estados inicial e final)
A aplicação da primeira lei ao tanque e compressor dá
que se integra a
Logo, esta é a saída de trabalho da turbina.
Passo 4
Note que, quando a primeira e segunda leis combinadas são reduzidas para caber na turbina e no sistema do tanque e o balanço de massa incorporado, o resultado é
onde o último passo usa a equação de mudança de entropia. Quando esta é integrada ao longo do processo, ela se torna
Esta é a energia da mudança do ar no tanque de armazenamento.