Uma libra de oxigênio, O2, é submetida a um ciclo de potência que consiste nos seguintes processos:
Processo 1-2: volume constante de p1 = 20 lbf/in2 (137,9 kPa), T1 = 500°R (4,6°C) para T2 = 820°R (182,4°C).
Processo 2-3: expansão adiabática até υ3 = 1,432υ2.
Processo 3-1: compressão a pressão constante até o estado 1.
Esboce o ciclo em um diagrama p–υ. Considerando comportamento de gás ideal, determine (a) a pressão no estado 2, em lbf/in2, (b) a temperatura no estado 3, em °R, (c) a quantidade de calor transferido e o trabalho, ambos em Btu, para todos os processos, e (d) a eficiência térmica do ciclo.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
O desenho do diagrama
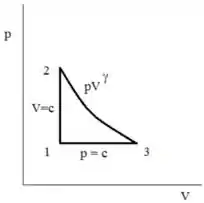
Passo 3
Calculando o volume inicial usando a equação do gás ideal
Passo 4
a) calculando a pressão no estado 2
Passo 5
b) Calculando o volume no estado 3
Calculando a pressão no estado 3 usando a relação adiabática
Agora, calculando a temperatura no estado 3
Passo 6
c) Calculando a mudança na energia interna para o processo 1-2
Calculando o trabalho feito para o processo 1-2
Calculando a transferência de calor para o processo 1-2
Passo 7
Calculando a mudança na energia interna para o processo 2-3
Calculando a transferência de calor para o processo 2-3
Calculando o trabalho feito para o processo 2-3
Passo 8
Calculando a mudança na energia interna para o processo 3-1
Calculando o trabalho feito no processo 3-1
Calculando o trabalho feito para o processo 3-1
Passo 9
d) Calculando o trabalho total
Calculando a eficiência térmica
Resposta
a)
b)
c)
d)