Um tanque rígido e isolado contendo inicialmente de vapor d’água saturado a 3,5 bar, é conectado por meio de uma válvula a um grande recipiente que armazena vapor a 15 bar e 320°C. A válvula é aberta apenas o tempo necessário para levar a pressão do tanque a 15 bar. Determine, para os conteúdos do tanque, a temperatura final, em °C, e a massa final, em kg.
Passo 1
Bora da aquele gás galera??
So vamooo!!!
Consideraremos a seguinte figura que mostra o volume de controle

Passo 2
- Escreveremos a equação de balanço de energia.
E uma vez que o único fluxo de massa que ocorre é o ar que entra no tanque, o equilíbrio da taxa de massa é de . Uma vez que não há nenhuma massa saindo do cilindro isolado então . E também o tanque e isolado não há nenhuma interação de calor então . Não há transferência de trabalho
Escreveremos a forma integral da equação de energia .
Passo 3
Aplicaremos a equação de balanço de massa para o volume de controle da seguinte maneira:
Substituindo .
Como o recipiente e muito grande , pode ser considerado constante.
Integre a equação (4) em relação ao tempo da seguinte maneira:
Passo 4
Substituindo na equação (5)
Passo 5
Partindo da tabela A-4, EM
Entalpia na entrada é
Uma vez que a condição final para o tanque rígido é 15 bar
A energia interna no estado 1 é .
O volume especifico no estado 1 é
A temperatura no estado 1 é de
Aqui há duas incógnitas , portanto, o solucionador de equações deve ser usado para a interpolação exata dos valores de acordo com a condição dada.
Uma vez que este é um problema baseado em computador, usaremos o solucionador de equações para resolver a equação (6) da seguinte maneira:
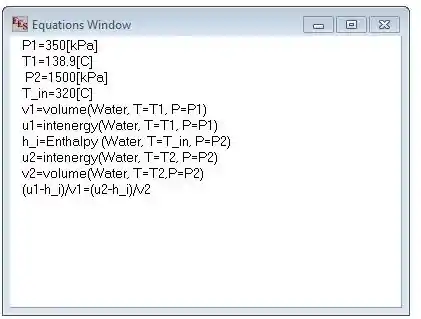

Portanto, a temperatura no estado 2 é de 362.2°C
Passo 6
Calculando a massa do sistema usando a seguinte expressão:
Portanto , a massa final no tanque é de 2.098 kg
Resposta
Portanto, a temperatura no estado 2 é de 362.2°C.
Portanto , a massa final no tanque é de 2.098 kg.