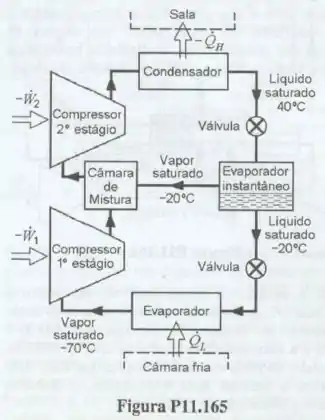
Uma maneira de melhorar o desempenho de um ciclo de refrigeração, que opera num grande intervalo de temperatura, consiste na utilização de um compressor de dois estágios. Considere o sistema ideal de refrigeração deste tipo, mostrado na , que utiliza como fluido de trabalho. Líquido saturado sai do condensador a e é estrangulado até . O líquido e o vapor, a esta temperatura, são separados e o líquido é estrangulado até a temperatura do evaporador . O vapor que sai do evaporador é comprimido até a pressão de saturação correspondente a . Após esta operação, ele é misturado com o vapor que sai da câmara de evaporação instantânea. Pode-se admitir que tanto a câmara de evaporação instantânea, como a câmara de mistura, estejam isoladas termicamente de modo a impedir qualquer transferência de calor do ambiente. O vapor que deixa a câmara de mistura é comprimindo, no segundo estágio do compressor, até a pressão de saturação correspondente temperatura do condensador . Nestas condições determine:
- O coeficiente de eficácia do ciclo.
- O coeficiente de eficácia de um ciclo ideal de refrigeração simples, que opera entre as mesmas temperaturas do condensador e do evaporador da unidade de compressão em dois estágios estudada neste problema.
Passo 1
Oi, tudo bem? Vamos resolver esta questão!
Neste problema queremos a fração de vapor extraído na turbina e a taxa de transferência de calor no condensador, considerando agora que a turbina seja real com um rendimento de .
Se você observar o exercício vai perceber que esta central de potência se comporta da seguinte maneira:
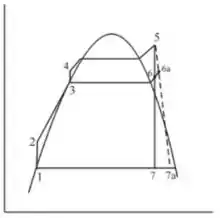
Vamos então organizar os dados:
Pressão máxima:
Pressão mínima:
Pressão do aquecedor de água de alimentação:
Temperatura máxima:
Eficiência isentrópica da turbina:
Potência de eixo da turbina:
Passo 2
Analisando os dados do estado e as tabelas termodinâmicas para o vapor supersaturado, temos que:
Analisando agora o estado de baixa pressão , das tabelas termodinâmicas conseguimos os seguintes dados:
Como o processo é isentrópico, podemos encontrar a entalpia do estado :
Passo 3
Agora vamos analisar a turbina de baixa pressão como sendo nosso volume de controle. Como temos o rendimento da turbina, sabemos que é uma turbina real. Neste caso vamos calcular os parâmetros para um processo ideal e depois aplicar o rendimento para saber a parcela real.
Analisando o processo ideal, , temos que:
Sabendo que na saída da turbina de baixa temos a mesma pressão de trabalho do condensador, podemos encontrar o título relacionado a este estado:
Aplicaremos o título para encontrar a entalpia especifica:
Passo 4
Agora para a turbina de alta pressão:
Passo 5
Sabendo a entalpia específica de entrada e de saída da turbina, podemos calcular o trabalho específico gerado:
Aplicando o rendimento podemos encontrar o trabalho de turbina real:
Como sabemos a potência de eixo, temos que:
Logo:
Passo 6
Já temos a vazão em massa e o trabalho específico gerado pela turbina. O exercício também nos pede a eficiência do ciclo.
A eficiência térmica é dada pela razão entre o trabalho líquido e o calor fornecido:
O trabalho líquido é a parcela de energia gerada menos a consumida. Neste ciclo o que consome trabalho é a bomba. O trabalho da bomba é dado por:
Ou:
Como , podemos encontrar o valor de . Temos que:
Passo 7
O calor fornecido pela caldeira é dado por:
Podemos então calcular a eficiência do ciclo:
Ou:
Ufa, conseguimos resolver. As questões que envolvem ciclos são bem extensas e necessitam de uma atenção redobrada nos dados, mas você já deve ter percebido que elas seguem um padrão. Seguindo o passo a passo você vai conseguir fazer várias questões desse tipo.
Vamos pra próxima?