Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 62

Para manter um motor a jato refrigerado, uma tomada de ar é feita externamente à câmara de combustão. Admita que 2   k g / s de ar quente a 2000   K e 500   k P a sejam misturados com 0,5   k g / s de ar a 500   K e 500   k P a sem qualquer transferência externa de calor. Determine a temperatura do ar na saída utilizando o calor específico constante da tabela A . 5 e repita o cálculo usando valores da tabela A.7

Passo 1

Fala galeraaa!

Vamos começar com a parte conceitual...

O primeiro passo é fazer o esboço para o nosso volume de controle...

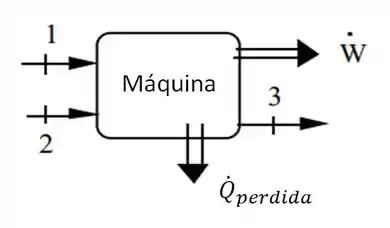
E como sabemos, num volume de controle temos a seguinte fórmula para a conservação de massa...

m ˙ 1 + m ˙ 2 = m ˙ 3

Logo, de cara podemos encontrar a vazão mássica em 3 na saída...

m ˙ 3 = 2   k g / s + 0,5   k g / s

m ˙ 3 = 2,5   k g / s

No caso, nosso processo ocorre sem qualquer transferência externa de calor... Dessa forma, nada é perdido e nem trabalho é gerado.

Passo 2

Pois muito bem! Já temos a vazão mássica na saída! Vamos então, pras outras condições...

Para o estado inicial... Nas condições 1 e 2... Das tabelas de vapor d’água superaquecido abaixo

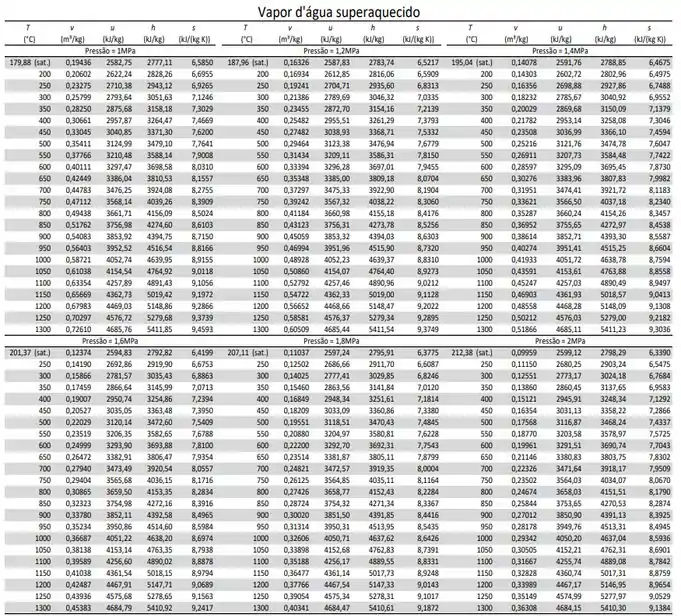
Temos os seguintes valores de entalpia...

E s t a d o   1 → 2000   K   o u   1727   ° C ,   500   k P a   ° C   ∴ h 1 = 2930,76   k J / k g

E s t a d o   2 → 500   K   o u   227   ° C , 500   k P a ∴ h 2 = 6588,86   k J / k g

Como podemos ver nas tabelas abaixo...

Passo 3

Assim, dada a vazão mássica na saída

Uma vez que sabemos a fórmula da energia, podemos obter a entalpia na saída...

m ˙ 1 h 1 + m ˙ 2 h 2 + Q = m ˙ 3 h 3

2 ⋅ 2930,76 + 0,5 ⋅ 6588,86 = 2,5 ⋅ h 3

h 3 = 3662,38   k J / k g

Assim, usando a fórmula da entalpia dada por...

h = c p T

Podemos encontrar a temperatura na saída...

3662,38 = 1,96 ⋅ T 3

T 3 = 3662,38 1,96 = 1868,56   K

Resposta

T 3 = 1868,56   K

Exercícios de Livros Relacionados

No circuito da Figura P7.78, a chave 1 estev na posição a, e a chave 2 esteve fechada, por um longo tempo. Em t = 0, a chave 1 passa instantaneamente para a posição b. Duzentos microssegundos mais tar
A fonte de corrente no circuito da Figura P7.81 (a) gera o pulso de corrente mostrado na Figura P7.81(b). Não há nenhuma energia armazenada em t=0.Deduza as expressões numéricas de v 0 ( t ) para os i
A forma de onda de tensão mostrada na Figura P7.82 (a) é aplicada ao circuito da Figura P7.82(b). A corrente inicial no indutor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função de
A chave no circuito da Figura P7.80 esteve na posição a por um longo tempo. EM t=0, ela passa instantaneamente para a posição b, onde permanece por 5 segundos antes de passar instantaneamente para a p
A forma de onda de tensão mostrada na Figura P7.84 (a) é aplicada ao circuito da Figura P7.84(b). A corrente inicial no capacitor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função d