Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 63

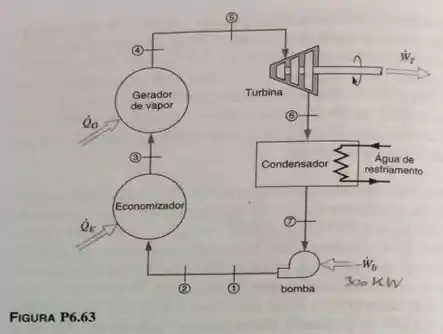
Os dados seguintes são para uma usina termelétrica simples a vapor conforme mostrado na Fig. P 6.63 . O estado 6 tem x 6 = 0,92 e uma velocidade de 200   m / s . A vazão de vapor é de 25   k g / s , com 300   k W de potência consumida pela bomba. Os diâmetros das tubulações são de 200   m m , do gerador de vapor até a turbina, e de 75   m m , do condensador até o economizador e gerador de vapor. Determine a velocidade no estado 5 e a potência de saída na turbina.

Passo 1

Fala galeraaa!

Vamos começar com a parte conceitual...

Sabemos que ss diâmetros das tubulações são de 200   m m , do gerador de vapor até a turbina, e de 75   m m , do condensador até o economizador e gerador de vapor...

Pois muito bem! Vamos começar calculando então, a área da seção transversal da turbina...

A 5 = π 4 d 2

Como...

d = 200   m m = 0,2   m

Então;

T u r b i n a ∴ A 5 = π 4 d 2 = π 4 0,2   m 2 = 0,03142   m ²

Passo 2

Pois muito bem! Sabendo então a área da turbina, vamos calcular a velocidade V 5 com que o vapor passa pela turbina no estado 5...

V 5 = m ˙ v 5 A 5

Onde o volume específico nas condições especificadas em 5, é dado por...

v 5 = 0,06163   m ³ / k g

Logo;

V 5 = 25 ⋅ 0,06113 0,03142

V 5 = 49   m / s

h 5 = 3404   k J / k g

Em seguida, vamos calcular o valor da entalpia no estado 6 dado que sabemos o título de 92 % :

h 6 = h 6 l + x ( h 6 v - h 6 l )

h 6 = 191,83 + 0,92 ⋅ 2392,8

h 6 = 2393,2   k J / k g

Passo 3

Assim, usando a equação de energia para o volume de controle em turbinas... Obtemos que:

w s a í d a + m ˙ h 6 + m ˙ V 6 2 2 = m ˙ h 5 + m ˙ V 5 2 2

W s a í d a + m ˙ h 6 + m ˙ V 6 2 2 = m ˙ h 5 + m ˙ V 5 2 2

W s a í d a = m ˙ h 5 - m ˙ h 6 + m ˙ ( V 5 2 - V 6 2 ) 2

Então, substituindo os valores numéricos encontramos nossa resposta...

W s a í d a = 25 3404 - 2393,2 - 200 2 - 49 2 2 ⋅ 1000

W s a í d a = 24805   k W

Resposta

W s a í d a = 24805   k W

Exercícios de Livros Relacionados

Argônio entra em regime permanente a 1600 kPa, 450 °C e uma velocidade de 55 m/s em uma turbina adiabática, saindo a 150 kPa com velocidade de 150 m/s. A área de entrada da turbina é de 60 c m 2 . Con
Uma turbina a gás adiabática expande um determinado volume de ar, inicialmente a 1300 kPa e 500 °C, para 100 kPa e 127 °C. Ar entra na turbina por uma abertura de 0,2 m 2 com uma velocidade média de 4
Uma mistura de líquido-vapor saturado de água, chamada de vapor úmido, inicialmente a 2000 kPa em uma linha de vapor, é estrangulada até uma pressão de 100 kPa e uma temperatura de 120 °C. Qual é o tí
Refrigerante-134a entra na válvula de expansão de um sistema de refrigeração a 160 psia como líquido saturado e sai a 30 psia. Determine as variações de temperatura e de energia interna ao longo da vá
Vapor escoa em regime permanente por uma turbina adiabática. Na entrada, o vapor está a 6 Mpa, 400 °C e 80 m/s, e na saída, a 40 kPa, 92% de título e 50 m/s. O fluxo de massa do vapor é de 20 kg/s. De