Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 66
Um diagrama de fluxo simplificado para uma usina termelétrica nuclear é dada na Fig. P6.66. As vazões mássicas e os vários estados no ciclo são mostrados na seguinte tabela:
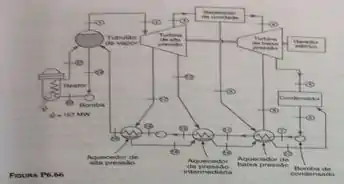
O ciclo inclui alguns aquecedores nos quais o calor é transferido do vapor extraído na turbina, a uma pressão intermediária, para a água líquida bombeada do condensador para o vaso de vapor. O trocador de calor no reator fornece , e pode se admitir que não existe transferência de calor nas turbinas.
- Considerando que não há transferência de calor no separador de umidade entre os dois estágios da turbina, determine a entalpia e o título
- Determine a potência de saída na turbina de baixa pressão
- Determine a potência de saída na turbina de alta pressão
- Determine a razão entre a potência de saída nas duas turbinas e a potência total fornecida pelo reator
Passo 1
Fala galeraaa!
Vamos começar simplificando o nosso volume de controle...
a) Vamos começar analisando o separador de umidade...
Considerando que não temos transferência de calor, então pela conservação de massa ficamos com...
Considerando o balanço de energia então;
Aí, podemos achar :
E assim, podemos encontrar o título correspondente para essa entalpia...
Passo 2
b) Em seguida, vamos atrás da potência de saída na turbina de baixa pressão...
No caso dando uma olhada na nossa figura, ficamos com...
Aí, substituindo os valores correspondentes podemos achar nossa resposta...
c)
E depois, da potência de saída na turbina de alta pressão...
Nesse caso, de acordo com a nossa figura, ficamos com...
E é a mesma coisa... Só substituir os valores correspondentes...
Passo 3
d) Por fim, falta achar a razão entre a potência de saída nas duas turbinas e a potência total fornecida pelo reator, no caso ...
Aí é só fazer o cálculo...
Pronto! Finalizamos aqui!
Resposta
a)
b)
c)
d)