Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 232
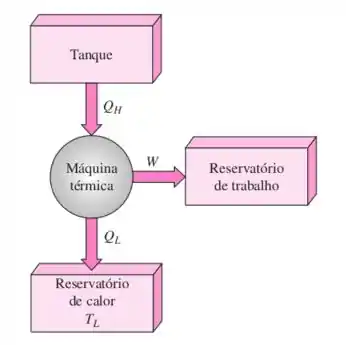
Uma máquina térmica recebe calor de um tanque de volume constante preenchido com 2 kg de ar. O trabalho produzido pela máquina é armazenado em um reservatório de trabalho; a máquina ainda rejeita 400 kJ de calor para um reservatório de calor a 300K. Durante o processo, a temperatura do ar no tanque diminui para 300 K. (a) Determine a temperatura inicial do ar que irá maximizar o trabalho e a eficiência térmica da máquina. (b) Avalie a variação total da entropia desse sistema isolado, o trabalho produzido e a eficiência térmica, considerando a temperatura inicial do ar no tanque do item (a) e também temperaturas 100 K acima e abaixo da resposta do item (a). (c) Trace a eficiência térmica e a geração de entropia como funções da temperatura inicial do ar. Comente suas respostas. Considere calores específicos constantes para o ar a 300 K.
Passo 1
Item A:
A variação de entropia para o tanque, cujo ar é considerado um gás ideal e cuja transferência de calor para a máquina térmica ocorre à volume constante é:
(1)
Uma vez que a transferência ocorre até que 
, ou seja, a temperatura do ar no tanque atinja a temperatura do reservatório, temos que:
(2)
Sendo 
, variação de entropia é determinada por:
(3)
com 
A entropia gerada é igual a variação total de entropia do sistema, sendo a soma da variação de entropia do reservatório com a variação de entropia do tanque. A variação de entropia para a máquina térmica é nula, de forma ao processo ser reversível e produzir o máximo de trabalho. Assim:
(5)
E a eficiência do processo pode escrita como:
(6)
Com $$Q_H$$ a energia sob forma de calor que o ar contido no tanque transfere à máquina térmica:
(7)
Resolvendo as equações (5), (6) e (7) simultaneamente utilizando um solver termodinâmico, os valores encontrados para temperatura inicial, eficiência da máquina, trabalho produzido e calor transferido pelo tanque à máquina térmica são:
Passo 2
item B:
Para a condição dada no item A, o trabalho e a eficiências são os maiores possíveis, uma vez que o processo ocorre de maneira reversível, com entropia gerada nula:
Para um estado de temperatura 100 K menor do que a temperatura encontrada no item A, a entropia produzida, a eficiências e o trabalho do processo são:
$$S_{gerada} = 0,2029 $$
$$\eta = 0,2245$$
$$W = 115,8 \: kJ $$
Observando os valores, vemos que ocorre o esperado: Uma temperatura menor para o gás acarreta a ocorrências de irreversibilidades no sistema, e por isso a entropia gerada é positiva. O trabalho e a eficiência então são menores do que no caso reversível.
Para um valor de temperatura 100 K maior do que a temperatura encontrada no item A, a entropia produzida, a eficiências e o trabalho do processo são:
$$S_{gerada} = -0,1777 $$
$$\eta = 0,5019$$
$$W = 403,0 \: kJ $$
Temos um valor negativo para a entropia gerada, o que revela a impossibilidade de ocorrência deste processo, com o sistema sobre essas condições.
Passo 3
item C:
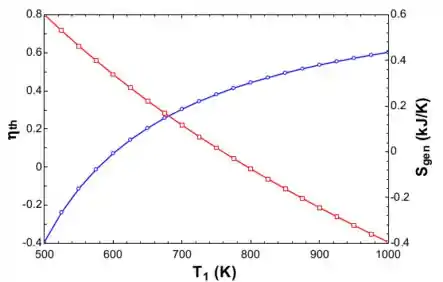
A eficiências térmica e a geração de entropia são plotadas como função da temperatura inicial estão plotadas no gŕafico a seguir:
Resposta
Ei, a resposta está no passo a passo :)