Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 84

O metano ( C H 4 ) é queimado com 300% de excesso de ar em um recipiente de volume constante adiabático. Inicialmente, ar e metano estão a 1 atm e 25 °C. Considerando uma combustão completa, determine a pressão e a temperatura final dos produtos da combustão.

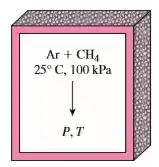
Passo 1

Vamos assumir que:

Os gases do ar e da combustão são ideais.

As energias cinética e potencial são desprezíveis.

Não há interações de trabalho.

A câmara de combustão é adiabática.

Passo 2

A equação da combustão é:

C H 4 + 4 a t h [ O 2 + 3.76 N 2 ] → C O 2 + 2 H 2 O + 4 a t h × 3.76   N 2 + 3 a t h O 2

onde a t h é o coeficiente estequiométrico e é determinado a partir do balanço de O 2 :

4 a t h = 1 + 1 + 3 a t h → a t h = 2

Substituindo:

C H 4 + 8 [ O 2 + 3.76 N 2 ] → C O 2 + 2 H 2 O + 30.08 N 2 + 6 O 2

Para esse processo de volume constante, o balanço de energia E e n t - E s a í d a = Δ E s i s t e m a aplicado na câmara de combustão reduz a Q = W = 0 levam à:

∑ N P ( h ̄ ° f + h ̄ - h ̄ ° - P v ̄ ) P = ∑ N R ( h ̄ ° f + h ̄ - h ̄ ° - P v ̄ ) R

Como os reagentes e os produtos são considerados gases ideais, toda a energia interna e entalpias dependem de somente temperatura e os termos P v nesta equação podem ser substituídos por R u T . Temos:

∑ N P ( h ̄ ° f + h ̄ - h ̄ ° - R u T ) P = ∑ N R ( h ̄ ° f + h ̄ - h ̄ ° - R u T ) R

Passo 3

Das tabelas:

Então:

h ̄ C O 2 + 2 h ̄ H 2 O + 6 h ̄ O 2 + 30.08 h ̄ N 2 - 324.9 T p = 1,047,514   k J

A temperatura adiabática da chama é obtida a partir de uma solução de tentativa e erro. Um primeiro palpite pode ser obtido assumindo que todos os produtos são nitrogênio e utilizam entalpia de nitrogênio na equação acima. Isso é,

39.08 h ̄ N 2 - 324.9 T p = 1,047,514   k J

Uma investigação da Tabela A-18 mostra que esta equação é satisfeita a uma temperatura próxima a 1200 K, mas estará um pouco abaixo dela devido ao maior calor específico do H 2 O .

À 1100K: 985,858   ( M e n o r   q u e   1,047,514   k J )

À 1200K: 1,089,662   ( M e n o r   q u e   1,047,514   k J )

Por interpolação:

T P = 1159   K

O volume de reagentes quando 1 kmol de combustível é queimado é:

V = V c o m b u s t í v e l + V a r = ( N c o m b u s t í v e l + N a r ) R u T P = 955.8   m 3

A pressão final é então:

P = N p r o d R u T V = 394   k P a

Resposta

T P = 1159   K

P = 394   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a capacidade térmica do corpo discutido na seção 5.6 seja 10J / K e T 1 = 200K . Calcule as variações na entropia do corpo e do reservatório, se T 2 = 400K T 2 = 600K T 2 = 100 K Mostre qu
Um resistor de 50 ohms termicamente isolado conduz corrente de 1 A por 1 s. A temperatura inicial do resistor é 10ºC, sua massa é 5 g e seu calor específico é 850 J/(K*Kg).Qual a variação de entropia
O círculo na figura 5.8 representa uma máquina reversível. Durante um número inteiro de ciclos a máquina absorve 1200 J de um reservatório a 400 K e realiza 200 j de trabalho mecânico. Encontre as qua
Um inventor afirma ter inventado uma máquina que aceitar 10 7 J a uma temperatura de 400 K, rejeita 4 E 6 J a uma temperatura de 200 K e libera 3,6 E 6 J de trabalho mecânico. Você aconselharia um inv
Um corpo de massa finita está originalmente a uma temperatura T 2 , que é maior que a um reservatório de calor a uma temperatura T 1 . Uma máquina funciona em ciclos infinitesimais entre o corpo e o r