Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 6.Problemas - Ex. 129
Um método promissor de geração de energia envolve a coleta e o armazenamento de energia solar em um lago artificial com poucos metros de profundidade, denominado lago solar. A energia solar e absorvida em todas as partes do lago, e a temperatura da água aumenta em todos os lugares. A parte de cima do lago, porém, perde para a atmosfera muito do calor absorvido, e por isso sua temperatura cai. Essa água fria serve como isolamento da parte de
baixo do lago e ajuda a aprisionar a energia. Em geral, coloca-se sal no fundo do lago para evitar que a água quente suba. Uma usina de energia que utiliza um fluido orgânico – álcool, por exemplo – como fluido de trabalho pode ser operada entre as partes de cima e de baixo do lago. Considerando que a temperatura da água seja de 35 °C nas proximidades da superfície e de 80 °C no fundo do lago, determine a eficiência térmica máxima que essa usina de energia
poderá ter. E realista utilizar temperaturas de 35 °C e 80 °C nos cálculos? Explique.
Passo 1
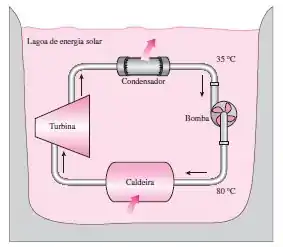
Vamos lá! A questão nos informa que uma central de energia solar funciona absorvendo o calor da região quente perto do fundo, e rejeitando o calor desperdiçado para a região fria perto do topo. A máxima eficiência térmica que a usina pode ter é a de ser determinada.
Então podemos representar como:
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. A maior eficiência térmica um motor térmico operando entre dois limites de temperatura especificados pode ter é a eficiência de Carnot, que é determinada de
Passo 3
Na realidade, a temperatura do fluido de trabalho deve estar acima de 35°C no condensador,
e abaixo de 80°C na caldeira para permitir qualquer transferência de calor eficaz. Portanto, a
a eficiência máxima do motor térmico real será inferior ao valor calculado acima.