Uma mistura com uma análise molar específica entra em um compressor operando em um estado estacionário em uma taxa de fluxo de massa específica e estado e sai em uma temperatura e pressão especificadas. Determine a potência necessária, a eficiência do compressor isentrópico e a taxa de destruição de energia.
Passo 1
CONHECIDO os dado a seguir temos:
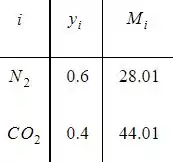
Passo 2
PREMISSAS: (1) O compressor está bem isolado e opera em estado estacionário.
(2) Os efeitos da energia cinética e potencial podem ser ignorados. (3) A mistura segue as idealizações do modelo de Dalton e a composição permanece constante. (4) Para o meio ambiente, T0 = 300 K.
ANÁLISE: A redução dos equilíbrios das taxas de massa e energia no estado estacionário da
Em que M é o peso da mistura molecular . Portanto, com dados a partir da tabela A23
Passo 3
Para determinar a eficiência do compressor isentrópico, é necessária a potência para uma compressão isentrópica do estado 1 à pressão P2 - ou seja, de 1 ao estado 25. Para este processo, .
. Então, com dados da tabela A23
resolver esta equação em qualquer iteração com os dados da tabela; T2s = 399k. Adequadamente
Passo 4
A eficiência do compressor isentrópico
A taxa de destruição de energia pode ser encontrada usando E d = T0 σ ˙ev, onde reduz no estado estacionário a f seguinte:
Os termos e são avaliados usando , so
Então, com dados dados a partir da tabela A 23
Passo 5
Multiplicando por
1 - Uma solução iterativa usando dados de tabela pode ser evitada usando TI. Os resultados para W ˙c, T2s, ηc e E d obtidos usando IT concordam com os valores dados aqui.
2 - quando exposta como uma porcentagem da entrada de energia para a compressão