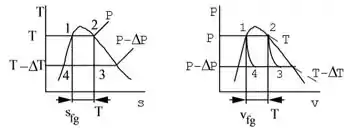
Em um motor térmico de Carnot, a adição de calor muda o fluido de trabalho de líquido saturado para vapor saturado em T, P. O processo de rejeição de calor ocorre em temperatura e pressão mais baixas (T - ∆T), (P - ∆P). O ciclo ocorre em um arranjo de cilindro de pistão onde o trabalho é um trabalho de limite. Aplique a primeira e a segunda lei com aproximações simples para a integral igual ao trabalho. Em seguida, mostre que a relação entre ∆P e ∆T resulta na equação de Clapeyron no limite ∆T → dT.
Passo 1
Salve galera, tudo tranquilo com vcs? 😊 Espero que sim! Bora pra essa questão que é tudo nosso!
![]()
Problema semelhante ao desenvolvimento na seção 13.1 para trabalho de eixo, aqui trabalho de movimento de limite,
![]()
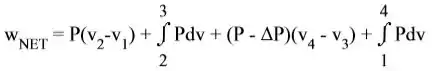
Passo 2
Aproximando:

Coletando termos:

(quanto menor o ∆P, melhor será a aproximação)
