Uma polia de 0,15 m de diâmetro movimenta uma correia fazendo girar o eixo motor da bomba de uma usina. O torque aplicado pela correia sobre a polia é de 200 N.m, e a potência transmitida é de 7 kW. Determine a força resultante aplicada pela correia sobre a polia, em kN, e a velocidade de rotação do eixo, em RPM.
Passo 1
Vamos começar dando uma desenhada nessa polia?
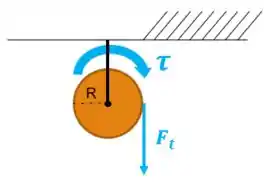
Onde pelo enunciado temos:
E para a potência temos a equação:
Mas não temos ainda nem a força, nem a velocidade né? Vamos calcula-las então!
Passo 2
Vamos calcular a força primeiro!
Você lembra qual a fórmula do torque? Se não lembra, deixa a gente te mostrar:
Onde o d é a distância do ponto de aplicação da força ao eixo de rotação. Então pra nossa situação, vamos ter:
Passo 3
Agora vamos para a velocidade! Temos para a potência a seguinte fórmula:
A análoga a ela para movimentos angulares, de rotação, é:
Vamos substituir nossos dados:
Mas vamos lembrar que a questão pediu em RPM! Vamos multiplicar por