Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 13.Problemas - Ex. 100
Um pré – aquecedor é alimentado com uma mistura de etileno com acetileno a e . A fração molar de etileno na mistura é e o pré – aquecedor descarrega a mistura a e . Determine o volume específico da mistura na seção de alimentação do equipamento utilizando a equação de Redlich – Kwong adequada para misturas. Recalcule o volume específico da mistura no mesmo local com a regra de Kay e o diagrama de compressibilidade generalizado.
Passo 1
E aí bonit@s, como vocês estão?
Se liguem só, precisaremos para nosso problema da constante dos gases. Para isso, vamos utilizar a equação do nosso livro, dada por
Passo 2
Pois bem, antes de utilizarmos a equação de Redlich Kwong precisamos calcular os parâmetros individuais dados por
Para a componente temos
Passo 3
Agora, precisamos dos parâmetros de mistura e para isso vamos precisar primeiramente das frações de massa que são dadas por
Sendo assim, nós poderemos calcular os parâmetros de mistura a partir da equação do livro que nos diz
Aplicando a fórmula vamos ter
Usando agora a equação teremos
Substituindo os valores numéricos vamos encontrar
Colocando em um software matemática vamos encontrar
Passo 4
Utilizando a regra de Kay vamos ter
Assim, nossas propriedades reduzidas serão
Utilizando o diagrama D1 teremos
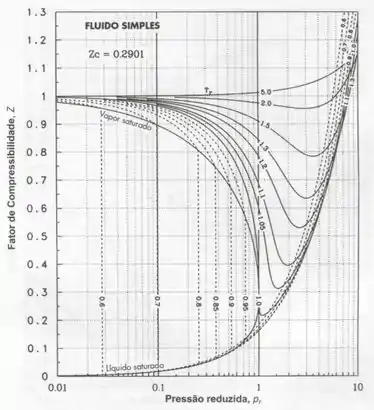
Apesar de estar um pouco ruim de ver vamos aproximar nosso fator de compressibilidade para e assim, encontraremos
Pronto, tá resolvido nosso problema.