Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 54
A pressão máxima num ciclo de potência a vapor d’água é . A temperatura no condensador do ciclo é e a caldeira descarrega o vapor a . Todos os componentes do ciclo, com exceção da turbina, são ideais. Sabendo que a temperatura real na seção de descarga da turbina é , determine a eficiência do ciclo (com a turbina real) e a eficiência isoentrópica da turbina.
Passo 1
Tudo bem? Preparado pra mais uma questão? Vamos lá!
Este exercício é parecido com o anterior. Temos um ciclo de potência com uma turbina real. E queremos a eficiência térmica e isentrópica desta turbina.
Um ciclo de potência a vapor é representado pelo seguinte diagrama T-s:
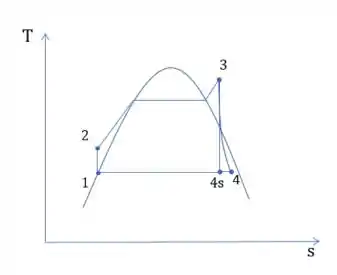
O caminho representa o processo isoentrópico realizado pela turbina e o processo real.
A partir da análise da tabela de propriedades termodinâmicas para o vapor de água, com e , temos que:
Como foi dito anteriormente, o processo é isoentrópico, portanto:
Como na saída da turbina temos que:
Podemos utilizar o valor da entropia e da temperatura do estado para descobrir o título e a entalpia específica. Primeiro vamos descobrir o título correspondente do estado :
A entalpia específica será:
Passo 2
Sabendo a entalpia específica do estado podemos encontrar o trabalho isentrópico da turbina:
O trabalho real da turbina é dado por:
A entalpia específica do estado é igual à de vapor saturado para a temperatura de
Passo 3
Portanto:
A eficiência isentrópica é dada por:
Vamos substituir os valores e calcular:
Passo 4
A eficiência térmica é dada pela razão entre o trabalho líquido e o calor fornecido, ou seja, da caldeira:
O trabalho líquido é dado pela subtração do trabalho produzido pelo trabalho gasto, ou seja, trabalho de turbina menos o trabalho da bomba:
A eficiência térmica será:
Isso aí, mais uma questão resolvida. Vamos para a próxima?