Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 86
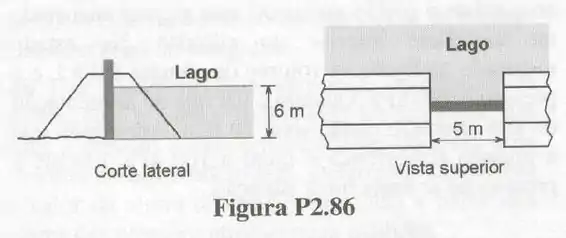
A profundidade do lago esboçado na Fig. P2.86 é igual a e a comporta vertical apresenta altura e largura respectivamente iguais a e . Determine os módulos das forças horizontais que atuam nas superfícies verticais externas da comporta.
Passo 1
Temos a seguinte situação:
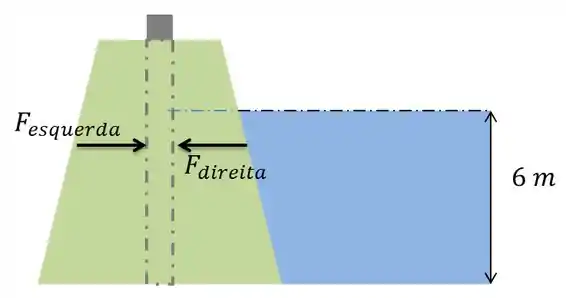
Temos que calcular é as forças atuando de cada face da nossa comporta.
A força da direita poderemos determinar pela coluna de água que nela está atuando.
Como Pressão é , podemos determinar a pressão da coluna de água e multiplicar pela área de contato na comporta e teremos a força da direita.
Quanto que a força da esquerda, pode ser determinada, por meio da pressão atmosférica. Pois, o material que temos encostado do lado esquerdo é apenas o ar.
Passo 2
Calculando a pressão da coluna de água, temos:
Considerando a densidade da água igual a , o cálculo fica:
Agora podemos determinar a força da direita:
Passo 3
Para a força da esquerda temos que a pressão atmosférica é considerada .