Reconsidere o Prob. 11–121E. O sistema de refrigeração do referido problema resfria um reservatório a 15 °F e outro a 40 °F enquanto rejeita calor para um reservatório a 80 °F. Qual dos processos tem a maior destruição de exergia?
Passo 1
Oi pessoal, tudo bem?
Bem, para o problema, podemos esboçar o diagrama T-s como:
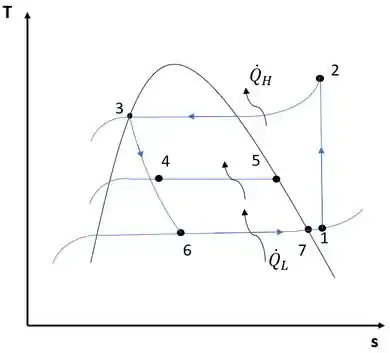
Bem, primeiramente, neste caso, vamos definir todas as entropias em cada estado analisado.
Passo 2
Assim, sabemos que o estado 3 se encontra em líquido saturado e possui e sabendo que o refrigerante é o R-134a, da tabela termodinâmica de líquido saturado:
E assumindo que há estrangulamento entre 3-4 e 4-6, temos
Uma vez que os estados 4 e 6 estão em mistura, e que e , devemos encontrar os seus respectivos títulos para posterior entropias, então podemos iniciar com:
Então:
E
Então:
O estado 5 encontra-se em vapor saturado e , então:
E o estado 7 encontra-se também em vapor saturado com , então:
Passo 3
Como vimos no problema anterior, para uma massa unitária que flui através do compressor, a fração de massa que flui através do evaporador II é indicada por x e que através do evaporador I é y (y = 1-x). De especificação de cargas de resfriamento:
Isolando termos:
Agora, de acordo com balanço de energia no ponto do sistema em que as duas correntes do evaporador são combinadas, temos:
Então, sabendo o valor de e sabendo que o estado 1 se encontra a , podemos encontrar o valor da entropia:
E como e sabemos do enunciado que , podemos encontrar a entalpia em 2:
Passo 4
A destruição da exergia durante um processo de fluxo de um estado de entrada para o estado de saída é dado por:
Portanto, aplicando a fórmula em cada componente do ciclo, temos:
Obs:
Obs: e
Obs: e
E por fim:
Resposta
Portanto a maior destruição da exergia ocorre durante o processo de mistura. Observemos que o calor é absorvido no evaporador 2 de um reservatório a , no evaporador 1 de um reservatório a e rejeitado para um reservatório a , que também é considerada a temperatura do estado morto.