Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 75
Uma grande indústria de processamento de alimentos requer 1,5 lbm/s de vapor de água saturado ou ligeiramente superaaquecido a 140 psia, o qual é extraído de uma turbina de uma usina de cogeração. A caldeira gera vapor a 800 psia e 1000 °F a uma taxa de 10 lbm/s, e a pressão do condensador é 2 psia. Vapor sai da unidade de processamento térmico como líquido saturado. Em seguida, é misturado com a água de alimentação à mesma pressão, e essa mistura é bombeada até a pressão da caldeira. Considerando que ambas as bombas e as turbinas têm eficiências isentrópicas de 86%, determine (a) a taxa de transferência de calor para a caldeira e (b) a potência produzida da usina de cogeração.
Passo 1
Beleza, antes de começar o exercício, vamos ilustrar o diagrama de uma usina de cogeração com seus equipamentos e pontos de interesse:
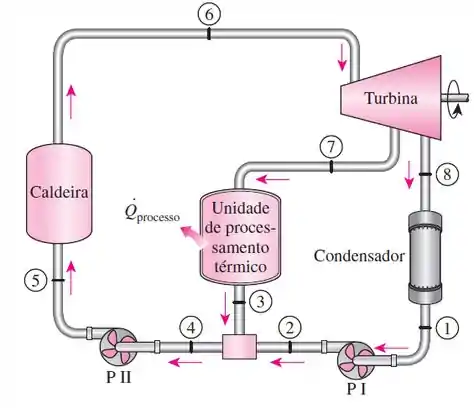
Tá legal! Agora, como o enunciado nos forneceu informações no sistema inglês, vamos converter os dados para o sistema internacional, então, temos:
Agora o que devemos fazer é pegar as propriedades do fluido nos pontos de interesse com os dados fornecidos no enunciado, então, com a ajuda das tabelas termodinâmicas do apêndice A, temos:
Com esse valor, podemos encontrar o trabalho específico exigido pela bomba 1 e depois encontrar a entalpia no ponto 2, então teremos:
E, aplicando o equilíbrio de energia específica para a bomba 1, temos:
Agora, continuando com as propriedades, temos:
Agora, para encontrar a entalpia no ponto 4, vamos aplicar o equilíbrio de energia para a câmara de mistura, então, teremos:
Nesse caso, como temos regime permanente, a equação acima se torna:
Então, aplicando essa equação para a câmara de mistura, temos:
Substituindo os valores conhecidos, temos:
Agora, com esse valor de entalpia e sabendo que no ponto 4 temos líquido, então, podemos pegar pela entalpia de saturação, recorrendo às tabelas termodinâmicas, teremos:
Com esse valor de volume específico, podemos encontrar o trabalho específico para a bomba 2 através de:
E, com isso, aplicando o equilíbrio de energia específica para a bomba 2, podemos encontrar a entalpia no ponto 5, então, teremos:
Passo 2
Agora, dando continuidade as propriedades no ponto de interesse, temos:
Com o valor da entropia do ponto 8, podemos encontrar o título nesse ponto:
E, com esse título, podemos encontrar a entalpia nesse ponto através de:
Passo 3
Agora vamos aplicar o equilíbrio de energia para a caldeira para descobrir a taxa de transferência de calor para ela, então, temos:
Substituindo os valores conhecidos, temos:
Passo 4
Agora, sabemos que podemos escrever a potência produzida pelo sistema em função da variação de entalpia na turbina (lembrando que nesse exercício temos que levar em consideração a eficiência isentrópica), então, teremos:
Substituindo os valores conhecidos, chegamos em: