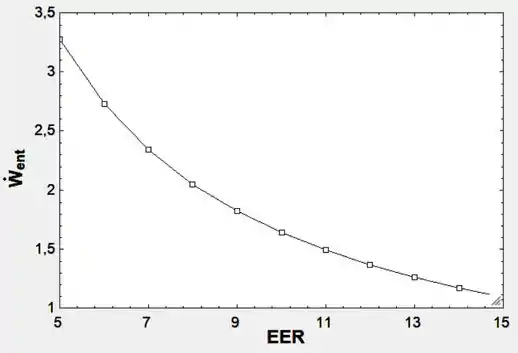
Reconsidere o Prob. 6–47. Usando o EES (ou outro programa), determine a potência necessária que o aparelho de ar condicionado deve ter para refrigerar a casa como uma função da REE de ar condicionado na faixa de 5 a 15. Discuta seus resultados e inclua os custos representativos de unidades de ar condicionado considerando a REE.
Passo 1
Oi pessoal, tudo bem?
Bem, para este tipo de problema, poderíamos utilizar o Excel para a geração do gráfico também (principalmente porque não necessitamos de propriedades termodinâmicas). Mas neste caso, vamos mostrar o gráfico gerado pelo software EES. Então, o problema é analisado da mesma forma do Prob. 6–47, com a diferença que o REE de ar condicionado terá uma variação na faixa de 5 a 15.
Passo 2
Vamos à linha de código a ser implementada no programa:
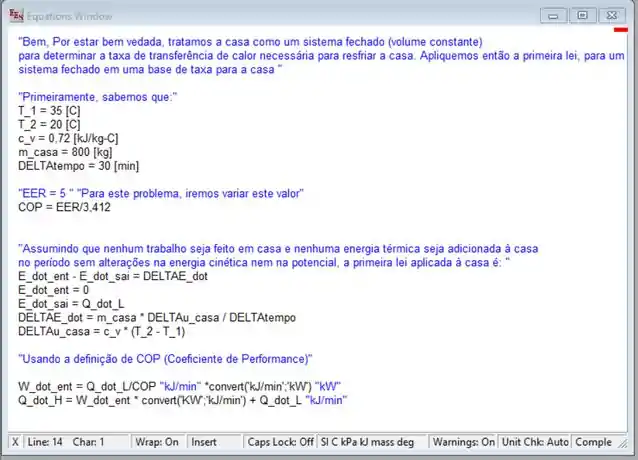
Passo 3
Utilizando as ferramentas do software, podemos encontrar o seguinte resultado:
- Analisando a variável “Retorno”, temos:
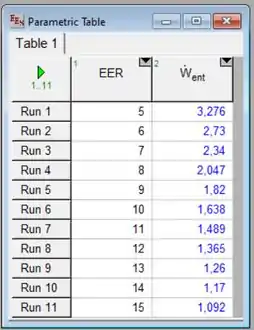
Resposta
Portanto, o gráfico gerado é: