Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 63
Repita o , considerando uma eficiência da compressão isentrópica equivalente a e uma eficiência de expansão isentrópica de .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O ciclo do enunciado é dado pelo seguinte diagrama:
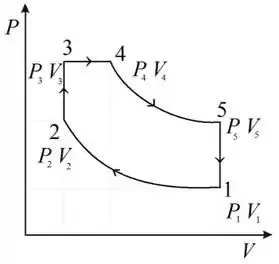
Nos foi dito que:
E:
Sabemos ainda que:
E:
Passo 2
Vamos agora encontrar as outras temperaturas envolvidas no ciclo. Para o processo de compressão. Temos que:
Como a razão de compressão é dada por:
Temos que:
Substituindo os valores, temos que:
Como a eficiência isentrópica de compressão é dada por:
Analogamente, temos que:
Passo 3
Analisando o processo :
Ou:
Como:
Temos que:
Substituindo os valores, temos que:
E:
Passo 4
Como , analisando agora o processo , temos que:
Analisando o diagrama, sabemos que:
Logo:
Que é a temperatura máxima do ciclo.
Passo 5
A pressão máxima também vai ocorrer no estado . Temos que:
Analisando o processo , temos que:
Como , temos que:
Aplicando a eficiência isentrópica para expansão, temos que:
Passo 6
Agora que temos todas as temperaturas envolvidas no ciclo, podemos calcular os calores de cada processo.
O calor de adição do processo é dado por:
Para o processo , temos que:
O calor total de entrada será:
O calor total de saída é dado pelo calor rejeitado no processo :
Logo:
Passo 7
De posse destes resultados podemos calcular a potência do ciclo:
Sendo:
Temos que:
Logo: