Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 99

Repita o P r o b .   9 – 98 considerando uma razão de pressão igual a 15 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Em questões de ciclos termodinâmicos é sempre bom desenhar o ciclo que se está utilizando para ajudar a identificar cada estado e processo envolvido.

Nessa questão por exemplo, trata-se do ciclo Brayton simples. Seu diagrama T - s é dado por:

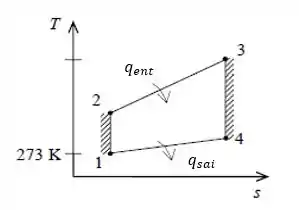
Primeiro vamos anotar os dados da questão:

r p = 1 5

T 1 = 273   K

P 1 = 70   k P a

Q ˙ e n t = 500   k W

m ˙ = 1   k g / s

Como devemos considerar calores específicos constantes a temperatura ambiente, podemos usar as relações envolvendo k para descobrir os dados que não sabemos.

Passo 2

O processo 1 → 2 é uma compressão isentrópica, logo:

T 2 T 1 = P 2 P 1 k - 1 k

Sabendo que:

P 2 P 1 = r p

Temos que:

T 2 = T 1 ⋅ r p k - 1 k

Substituindo os valores temos que:

T 2 = 273 ⋅ 1 5 1,4 - 1 1,4

T 2 = 5 91,818   K

Passo 3

Para descobrir a temperatura no estado 3 podemos analisar o processo 2 → 3 de entrada de calor. Temos que:

Q ˙ e n t = m ˙ c p T 3 - T 2

Isolando para T 3 , temos que:

T 3 = T 2 + Q ˙ e n t m ˙ ⋅ c p

Substituindo os valores conhecidos, temos que:

T 3 = 591,818 + 500 1 ⋅ 1,005

T 3 = 1 0 89,33   K

Passo 4

O processo 3 → 4 é uma expansão isentrópica, logo:

T 4 T 3 = P 4 P 1 k - 1 k

Sabendo que:

P 2 P 1 = P 3 P 4 = r p

Temos que:

T 4 = T 3 ⋅ 1 r p k - 1 k

Substituindo os valores temos que:

T 4 = 10 89,33 ⋅ 1 1 5 1,4 - 1 1,4

T 4 = 502,496   K

Passo 5

Agora que sabemos as temperaturas de cada estado, podemos calcular os trabalhos de turbina e compressor quando forem isentrópicos.

Para o compressor isentrópico, temos que:

w c o m p = c p T 2 - T 1

w c o m p = 1,005 ⋅ 5 91,818 - 273

w c o m p = 320,41   k J / k g

Para a turbina isentrópica, temos que:

w t u r b = c p T 3 - T 4

w t u r b = 1,005 ⋅ 1089,33 - 502,496

w t u r b = 589,77   k J / k g

A potência produzida será:

W ˙ l i q = m ˙ w t u r b - w c o m p

Resolvendo, temos que:

W ˙ l i q = 1 ⋅ 589,77 - 320,41

W ˙ l i q = 269,36   k W

Passo 6

A eficiência térmica é dada por:

η = W ˙ l i q Q ˙ e n t

Portanto, a eficiência térmica será:

η = 269,36   500

η = 0 , 5387

Ou:

η = 53,87 %

Resposta

W ˙ l i q = 269,36   k W

η = 53,87 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ciclo de turbina a gás tem dois estágios de compressão, com um intercooler entre os estágios. O ar entra no primeiro estágio a 100 kPa, 300 K. A razão de pressão em cada estágio do compressor é de
A turbina em um motor a jato recebe ar a 1250 K, 1,5 MPa. Ele esgota em um bocal a 250 kPa, que por sua vez escoa para a atmosfera a 100 kPa. A eficiência isentrópica da turbina é 85% e a eficiência d
Um compressor de dois estágios em uma turbina a gás traz o ar atmosférico a 100 kPa, 17oC a 500 kPa, e então o resfria em um intercooler a 27oC em P. constante. O segundo estágio traz o ar a 1000 kPa.
Repita as perguntas do Problema 11.75 quando presumimos que o atrito causa quedas de pressão no queimador e em ambos os lados do regenerador. Em cada caso, a queda de pressão é estimada em 2% da press
Considere um ciclo Ericsson de padrão aéreo ideal que tenha um regenerador ideal, conforme mostrado na Fig. P11.85. A alta pressão é de 1 MPa e a eficiência do ciclo é de 70%. O calor é rejeitado no c