Repita o Prob. 15–115 utilizando um carvão de Utah (Estados Unidos), cuja análise final (em massa) corresponde a , , , 1 , e de cinzas (não combustíveis). Despreze o efeito do enxofre nos balanços de energia e entropia.

Com isso, podemos escrever a equação de combustão da seguinte forma:

De acordo com o balanço do oxigênio, temos:

Substituindo:

O peso aparente vai ser dado por:

Agora, temos que:

Assumindo que o ar e a combustão produzem um gas ideal, teremos . A partir da tabela abaixo, temos:

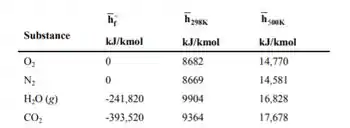
Logo:

Com isso, temos que a perda de calor por unidade de massa do combustível é dada por:

Por fim, a quantidade de vapor gerado por unidade de massa de combustível queimado é determinada a partir de um balanço energético, temos:

Agora, para calcularmos a geração de entropia durante este processo, temos:

Os valores de entropia listados nas tabelas de gás ideais são para pressão de . Tanto o ar quanto o gás do produto estão no total, com pressão de , mas as entropias devem ser calculadas à pressão parcial dos componentes que é igual a , onde é a fração molar do componente . Então:

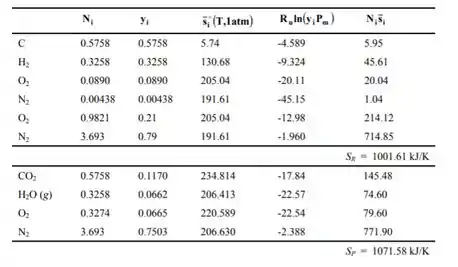
Substituindo:

Sabemos que a mudança de exergia dos fluxos de combustão é igual à destruição de exergia, uma vez que não há saída real do trabalho. Temos:

Por unidade de massa, temos:

Agora, para a mudança de exergia da corrente de vapor, temos:

Por fim, o potencial de trabalho perdido é o negativo da variação líquida de exergia de ambos os fluxos. Logo: