Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 34

Um tanque rígido é dividido em duas partes iguais por uma partição. Uma parte do tanque contém 4 kg de água líquida comprimida a 200 kPa e 80 °C, enquanto a outra parte está evacuada. A partição é então removida e a água se expande preenchendo todo o tanque. Considerando que a pressão final do tanque é de 40 kPa, determine a exergia destruída durante esse processo. Considere a vizinhança a 25 °C e 100 kPa.

Passo 1

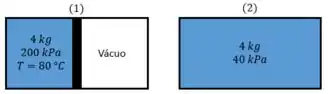
Em ambos os casos temos líquidos comprimidos. Valos usar as tabelas termodinâmicas para calcular as propriedades P 1 = 200   k P a T 1 = 80   º C ⇒ T a b e l a   A - 4 v l = 0,001029 m 3 k g u l = 334,97 k J k g s l = 1,0756 k J k g   K

Quando a partição é removida o volume dobra e a massa continua constante. Logo, podemos dizer que:

v 2 = 2 ⋅ v 1 = 0,002058 m 3 k g

Ao mesmo tempo, a pressão no recipiente é dada pela questão. Ao consultar a Tabela A-5 percebemos que estamos numa região de mistura:

P 2 = 40   k P a v 2 = 0,002058 ⇒ T a b e l a   A - 5 v l = 0,001026   m 3 k g v v = 3,9933   m 3 k g u l = 317,58 k J k g u l v = 2158,8 k J k g s l = 1,0261 k J k g   K s l v = 6,6430 k J k g   K

Com isso podemos calcular o título e depois as demais propriedades

x 2 = 0,002058 - 0,001026 3,9933 - 0,001026 = 0,0002584

u 2 = u l + x 2 ⋅ u l v = 317,58 + 0,0002584 ⋅ 2158,8 = 318,14 k J k g

s 2 = s l + x 2 ⋅ s l v = 1,0261 + 0,0002584 ⋅ 6,6430 = 1,0278 k J k g   K

Passo 2

Vamos aplicar a primeira lei da termodinâmica

Q - W = Δ U

Durante o processo não há transferência de trabalho, então:

Q = Δ U

Q = m u 2 - u 1

Q = 4 ⋅ 318,14 - 334,97

Q = - 67,30   k J

Durante o processo, o fluido perde calor para o ambiente.

Q s a i = 67,3   k J

Passo 3

Agora vamos calcular a entropia gerada no processo:

S e n t - S s a i + S g e r = Δ S

0 - Q s a i T 0 + S g e r = m ( s 2 - s 1 )

S g e r = m s 2 - s 1 + Q s a i T 0

S g e r = 4 1,0278 - 1,0756 + 67,3 298

S g e r = 0,03464   k J

Passo 4

E finalizamos a questão calculando a exergia destruída

X d e s t r = T 0 ⋅ S g e n

X d e s t r = 298 ⋅ 0,03464

X d e s t r = 10,32   k J

Resposta

X d e s t r = 10,32   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

56 Calcule as variações de disponibilidade em kW, nos dois escoamentos descrito no Prob. 9.61.
66 Um bloco de cobre, com massa igual a 1 kg, inicialmente apresentava temperatura uniforme e igual a 350°C. O bloco foi submerso num banho de óleo, que inicialmente estava a temperatura ambiente (20°
55 Um trocador de calor é alimentado com ar a 1500 K e 100 kPa. A queda de pressão no escoamento de ar no trocador é nula e o trocador opera como fonte quente de uma máquina térmica que rejeita calor
70 Um compressor é alimentado com vapor saturado de R-134a a -20°C e descarrega o fluido a 30 °C e 0,4 MPa. Admitindo que o compressor é adiabático, determine a eficiência isoentrópica e a eficiência
62 O trocador de calor mostrado na Fig. P10.62 é alimentado com água líquida saturada a 200 kPa. O escoamento de água no trocador não apresenta perda de carga e a transferência de calor para a água é