Um tijolo de 2,5 3,5 6 in (0,06 0,09 0,15 m), cuja massa específica é 120 lb/ft³(1922,2 kg/m³) escorrega do topo de um edifício em construção e cai 69 ft (21,0 m). Para g = 32,0 ft/s² (9,7 m/s²), determine a variação na energia potencial gravitacional do tijolo, em ftlbf.
Passo 1
Vamos resolver mais essa, pessoal. Um tijolo cai 69 ft do topo de um edifício. Observando a figura, que mostra um esquema para esse problema, vamos considerar que a altura final do tijolo é igual a altura de referência (z = 0). Assim, a variação de energia potencial será negativa.
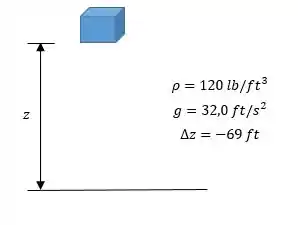
Antes da gente ir para as contas, vamos lembrar a fórmula para calcular a variação de energia potencial
Passo 2
Agora vamos descobrir o que falta para a gente usar a equação de energia potencial, que nesse caso é a massa. Vamos lembrar de um conceito interessante, a massa específica, que é
Com as dimensões do tijolo, podemos calcular o seu volume, V. Como as dimensões estão em polegadas, vamos dividi-las por 12, para converter em pés. Com isso,
Assim
Passo 3
Com todos os dados na mão, a gente pode calcular a variação de energia potencial
Convertendo para