Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 107
Uma turbina adiabática opera com ar entrando a e e saindo a e . Calcule a eficiência de segunda lei dessa turbina. Considere .
Passo 1
Vamos lá, estudantes! O ar se expande em uma turbina adiabática de um estado especificado para outro estado especificado. A eficiência da segunda lei deve ser determinada. A temperatura média de , o calor específico de pressão constante do ar é (Tabela A-2b). A constante de gás do ar é (Tabela A-1).
Passo 2
Há apenas uma entrada e uma saída, e assim . Tomamos a turbina como o sistema, que é um volume de controle, já que a massa atravessa o limite. O balanço energético para este sistema de fluxo constante pode ser expresso na forma de taxa como
A substituir,
Passo 3
A mudança de entropia do ar é
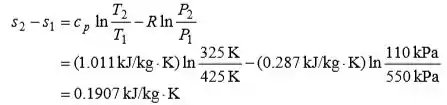
O trabalho máximo (reversível) é a diferença de esforço entre os estados de entrada e saída,
A eficiência da segunda lei é então
