Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 157
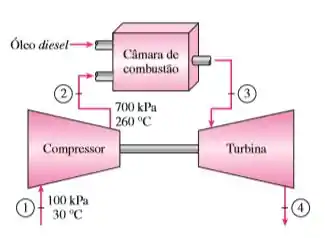
Uma usina de potência com turbina a gás funciona segundo o ciclo Brayton simples entre os limites de pressão de 100 kPa e 700 kPa. Ar entra no compressor a 30 °C a uma vazão de 12,6 kg/s e sai a 260 °C. Óleo diesel com um poder calorífico de 42.000 kJ/ kg é queimado na câmara de combustão com uma razão ar-combustível de 60 e uma eficiência de combustão de 97%. Os gases de combustão saem da câmara de combustão e entram na turbina, cuja eficiência isentrópica é de 85%. Tratando os gases de combustão como ar e considerando calores específicos constantes a 500 °C, determine
- a eficiência isentrópica do compressor
- a potência líquida produzida e a razão de consumo de trabalho
- a eficiência térmica
- a eficiência de segunda lei.
Passo 1
Vamos assumir que:
As premissas do padrão aéreo são aplicáveis.
As alterações cinéticas e potenciais de energia são insignificantes.
O ar é um gás ideal com aquecimentos específicos constantes.
Sabemos que as propriedades do ar a 500ºC são:
Passo 2
Vamos analisar:
Na letra a, a eficiência isentrópica do compressor pode ser determinada se primeiro calcularmos a temperatura de saída para o caso isentr��pico:
Passo 3
Na letra b, a massa total que flui através da turbina e a taxa de entrada de calor são:
A temperatura na saída da câmara de combustão é:
A temperatura na saída da turbina é determinada usando a relação de eficiência isentrópica
A potência líquida e a taxa de retrabalho são
Passo 4
Na letra c, a eficiência térmica é:
A eficácia da segunda lei do ciclo é definida como a razão entre a eficiência térmica real e a máxima eficiência térmica possível (eficiência de Carnot). A temperatura máxima para o ciclo pode ser considerada a temperatura de entrada da turbina. Isso é,
e