Uma usina de potência a vapor opera em um ciclo de Rankine generativo ideal com dois aquecedores de água de alimentação abertos. O vapor entra na turbina a 10 Mpa e 600 °C e é descarregado para o condensador a 5 kPa. Vapor é extraído da turbina a 0,6 MPa e 0,2 MPa. A água sai de ambos os aquecedores de água de alimentação como líquido saturado. O fluxo de massa do vapor na caldeira é de 22 kg/s. Mostre o ciclo em um diagrama T-s e determine (a) a potência líquida da usina e (b) a eficiência térmica do ciclo.
Passo 1
Para nos ajudar a visualizar o problema, vamos esquematizar o ciclo com regeneador duplo:
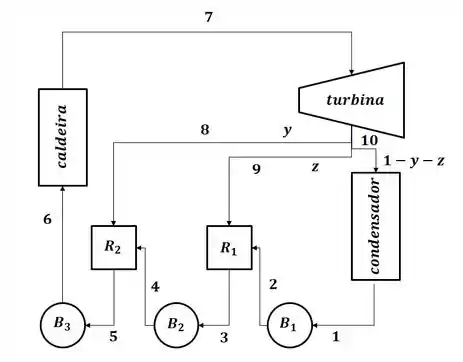
E o diagrama Ts do sistema será:
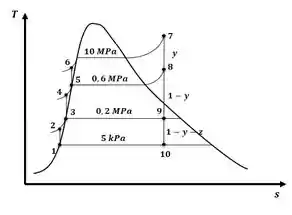
A primeira coisa que temos que fazer é pegar o valor das propriedades nos pontos de interesse, então teremos:
Para o ponto 9, precisamos calcular o título, então, temos:
Da mesma forma, para obter a entalpia, temos:
Agora para o ponto temos:
Calculando o título, temos:
E, para a entalpia, temos:
Passo 2
Agora, vamos calcular o trabalho nas bombas e descobrir as entalpias nos pontos restantes, então, para a bomba 1, temos:
Dessa forma, aplicando o equilíbrio de energia para a bomba 1, temos:
Agora, calculando o trabalho específico para a bomba 2:
Dessa forma, aplicando o equilíbrio de energia para a bomba 2, temos:
E, por fim, para a bomba 3:
Dessa forma, aplicando o equilíbrio de energia para a bomba 1, temos:
Passo 3
Agora nós vamos aplicar o balanço de energia para o regenerador 2 do passo 1, então, temos:
Nesse caso temos regime permanente, então , dessa forma a equação se torna:
E analisando o regenerador 2, teremos:
Com a relação mássica para o regenerador 2 temos:
Substituindo os valores conhecidos, temos:
Agora, para o regenerador 1, fazendo a mesma análise, temos:
E analisando o regenerador 1, teremos:
Com a relação mássica para o regenerador 1 temos:
Substituindo os valores conhecidos, temos:
Passo 4
Agora, vamos aplicar o balanço de energia específica para a caldeira, temos:
Substituindo os valores conhecidos, temos:
Agora, aplicando o balanço de energia para o condensador, temos:
Substituindo os valores conhecidos:
Dessa forma, o trabalho específico do sistema será:
Então, a potência produzida pela turbina será:
Passo 5
E, por fim, para a letra b), para encontrar a eficiência térmica do sistema, faremos: