Uma usina de potência a vapor opera no ciclo de Rankine com reaquecimento. Vapor de água entra na turbina de alta pressão a 12,5 MPa e 550 °C a uma vazão de 7,7 kg/s, saindo a 2 MPa. Em seguida, o vapor é reaquecido a uma pressão constante até 450 °C antes de se expandir na turbina de baixa pressão. As eficiências isentrópicas da turbina e da bomba são de 85% e 90%, respectivamente. O vapor deixa o condensador como líquido saturado. Considerando que o conteúdo de umidade do vapor na saída da turbina não deve exceder 5%, determine (a) a pressão no condensador, (b) a potência líquida produzida e (c) a eficiência térmica.
Passo 1
Oi pessoal, tudo bem?
Consideremos o esboço para este problema:
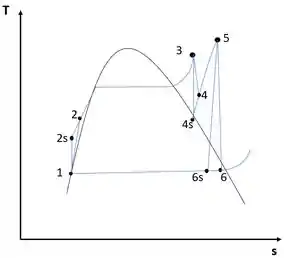
Bem, utilizando o auxílio das tabelas A.4, A.5 e A6, é possível encontrar algumas relações termodinâmicas para a resolução deste problema e dos outros desse capítulo.
Passo 2
O problema não traz informações inicias acerca da pressão ou temperatura no estado 1, impossibilitando de calcularmos a entalpia agora, assim como do estado 2, que depende do estado 1.
Mas sabemos que e que o estado 3 é vapor superaquecido, então:
Passo 3
E sabemos que e que , portanto, das tabelas:
Devemos lembrar que a eficiência da turbina pode ser escrita:
Para o estado 5, sabemos a pressão e temperatura , e que está em vapor superaquecido, então:
No estado 6, temos somente, e sabemos que . Neste caso temos duas equações com duas incógnitas: .
Mas, assim como no estado 3, porém agora analisando a eficiência da bomba, temos:
A pressão no estado 6 pode ser determinada por uma abordagem de tentativa-erro das tabelas de vapor ou usando o EES das três equações acima. Assim, podemos encontrar que:
Passo 4
Agora, como sabemos e , estando o estado 1 em líquido saturado, podemos encontrar as propriedades nas tabelas termodinâmicas:
Sabendo que o trabalho específico pode ser dado por :
Passo 5
Então, o calor que entra é:
E o calor que sai:
Assim, a potência do ciclo é:
E a eficiência térmica:
Resposta
Portanto: