Carta psicrométrica
Teoria
Carta psicrométrica simplificada
Quando vimos psicrometria a gente viu um monte de fórmula e jeitos de calcular a umidade relativa, absoluta, entalpia e outras grandezas, correto? Além disso é muito raro estudar essa matéria com uma mistura sem ser ar-vapor d’água a pressão atmosférica.
Sendo assim, algumas grandezas ficam fixadas como por exemplo a relação entre as massas moleculares:
Então a tal da carta psicrométrica foi criada para nos poupar do trabalho de ficar calculando várias grandezas. Essa carta nada mais é do que um gráfico com diversos eixos mas antes de ver como ela é de fato vamos mostrar um esboço com apenas os eixos de umidade absoluta e temperatura de bulbo seco.
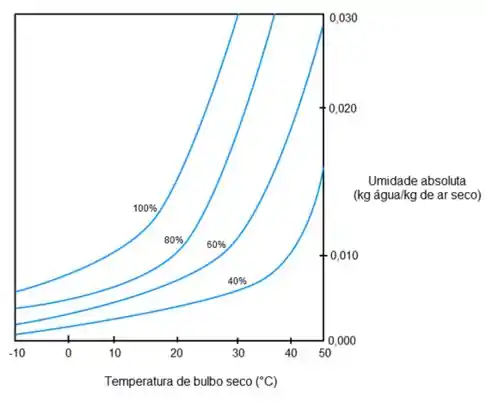
Olha só como no eixo horizontal temos as temperaturas de bulbo seco, no vertical a umidade absoluta e as curvas relativas a cada umidade relativa (em porcentagem). Olhando esse esboço vemos que com duas grandezas podemos achar a terceira.
Mas a carta real não é bem assim, é um pouco chata de entender de primeira porque é muito “poluída” com informações. Mas isso não é ruim, porque quanto mais informações melhor, só precisa ficar atento para entender todas.
Carta psicrométrica real
A carta psicrométrica de verdade vai possuir algumas informações a mais né? São elas: Entalpia específica do ar úmido, temperatura de bulbo úmido e volume específico da mistura.
Caraca, então no gráfico que já tínhamos três grandezas vamos ter mais três? Sim! É isso aí mesmo, então presta atenção para como vai ficar.
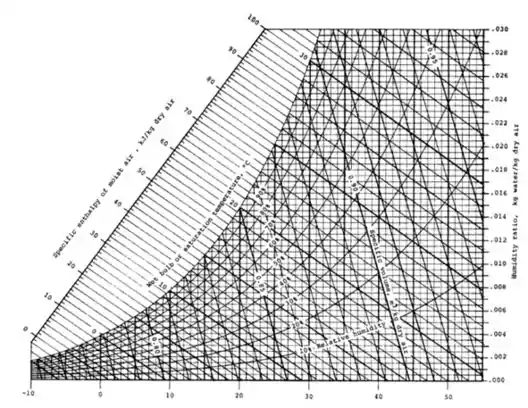
O eixo horizontal continua sendo o da temperatura de bulbo seco, assim como o vertical a umidade absoluta e as curvas a umidade relativa.
O que temos a mais aqui é a entalpia específica do ar úmido, que aparece na parte de cima à esquerda (é uma reta um pouco inclinada) e a temperatura de bulbo úmido. A graduação da temperatura de bulbo úmido é paralela à da entalpia específica a única coisa que muda é a escala. Dá uma olhada só a figura abaixo para entender um pouco melhor.
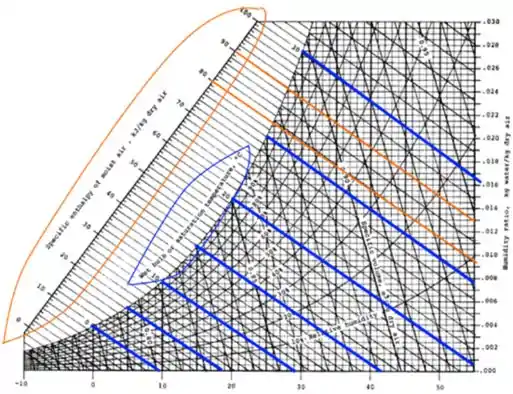
A entalpia está mostrada a cima em laranja e a temperatura de bulbo úmido abaixo em azul. Repara que a entalpia tem graduação de 0 a 100 mais ou menos, enquanto a temperatura de bulbo úmido é de -10 a 32 mais ou menos.
Nessa figura as linhas foram traçadas e fica bem evidente que elas são paralelas então é preciso ter um pouco de cuidado para não confundir. A dica é a seguinte, para a entalpia os valores são representados longe das curvas enquanto para a temperatura de bulbo úmido os valores são representados exatamente em cima da curva de umidade relativa igual a 100%.
Volume específico
Para finalizar só faltou o volume específico
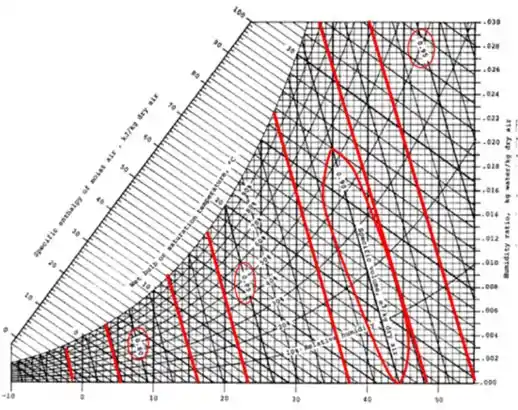
Então aqui representamos, em vermelho, as linhas de volume específico da mistura, viu como elas bem mais inclinadas do que as outras retas? Além disso, foram representados também 4 círculos (ok, 3 círculos e uma elipse bizarra) que mostram os valores. Indo do menor (mais embaixo e mais à esquerda) até o maior (mais no alto e à direita) eles tem, os valores de 0,8 – 0,85 – 0,90 e 0,95, respectivamente.
Essa parte da carta é a que você provavelmente vai usar menos, mas agora você tem o conhecimento completo dessa ferramenta.
Vamos fazer um exemplo antes de partir para os exercícios!
Dada a carta psicrométrica e o ponto representado abaixo. Determine a umidade relativa, a umidade absoluta, a temperatura de bulbo seco, a temperatura de bulbo úmido, a entalpia específica e o volume específico.
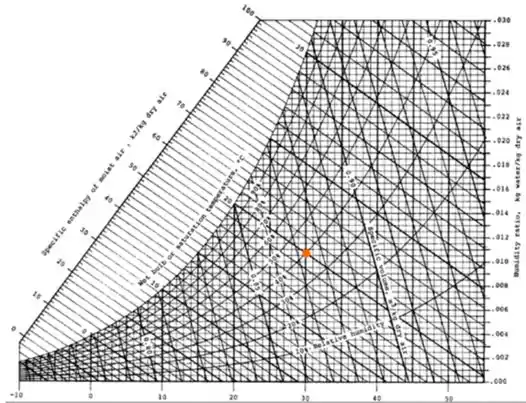
Show! Vamos fazer o seguinte, vamos quebrar o exercício em duas partes. Na primeira vamos achar as temperaturas de bulbo seco e úmido, umidade relativa e absoluta, na segunda a entalpia e volume específico.
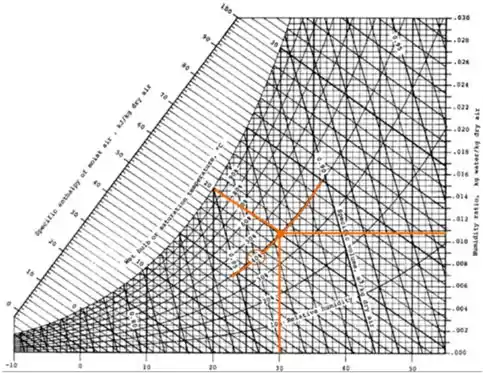
- Temperatura de bulbo seco – Representada pela reta vertical = 30°C.
- Umidade absoluta – Representada pela reta horizontal = 0,019 kg de água / kg de ar seco.
- Temperatura de bulbo úmido – Representada pela reta inclinada = 20°C.
- Umidade relativa – Representada pela curva = 40%.
Vamos para a segunda parte agora:
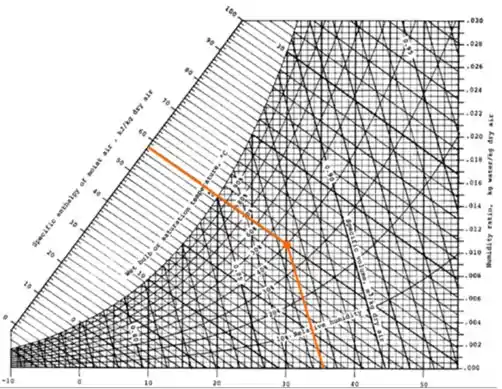
- Entalpia específica do ar úmido – Representado pela reta inclinada para cima e para a esquerda = 58 kJ / kg de ar seco.
- Volume específico – Representado pela reta inclinada para baixo e para a direita = 0,875 m³ / kg de ar seco. (Aqui vale uma observação de que os valores ficam muito distantes um do outro, mas da para reparar que essa reta se econtra entre a de 0,85 e a de 0,90).
Partiu exercícios!
Carta psicrométrica real
Volume específico
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Na carta psicrométrica a temperatura de bulbo úmido é mostrada bem próxima à curva de umidade relativa igual a 100%, porque ela é feita assim?
Passo 1
Isso acontece porque a própria temperatura de bulbo úmido é a temperatura num estado de saturação da mistura ar-vapor d’água, ou seja, umidade relativa igual a 100%. Portanto, não faria sentido representa-lá em outro lugar.
É importante lembrar também que neste caso de umidade relativa 100% (estado de saturação) as temperaturas de bulbo seco e úmido são iguais.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Você provavelmente já ouviu falar que é perigoso fazer esportes num dia muito quente e com alta umidade. Imagine a situação de uma pessoa sair para correr num dia em que a temperatura esteja em 40°C e a umidade relativa de 100%, qual seria o perigo relacionado à essa atividade?
Passo 1
A primeira coisa que devemos lembrar é o fato do corpo humano trabalhar na temperatura de 36,5°C. Ou seja, a temperatura ambiente esta a cima da temperatura corporal. Porém, esse não é o problema porque ao transpirar o efeito de resfriamento evaporativo pode reduzir essa temperatura de 40°C para uma temperatura mais amena.
O grande problema se encontra no fato da umidade relativa estar em 100%. Se o ar encontra-se saturado de vapor d’água ele não aceitara mais vapor, logo o suor não evapora e o efeito de resfriamento não ocorre. Sendo assim, o nosso corredor sofre o risco de elevar sua temperatura corporal o que pode causar danos à saúde.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Seria possível representar outras propriedades na carta psicrométrica fora as já representadas abaixo? Porque?
Passo 1
Sim. Porque são necessárias 3 propriedades para definir o estado termodinâmico (três porque é um mistura então mais uma propriedade é necessário do que as duas que estamos acostumados), porém, como a pressão está fixada em 100 kPa (atmosférica).
Assim, com mais duas propriedades, por exemplo, temperatura e umidade o estado termodinâmico se encontra fixo. Com isso todas as outras propriedades também se fixam.
Se todas as propriedades estão fixas podemos incluir a propriedade que quisermos, como a entropia por exemplo.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
UNICAMP, Introdução à psicrometria parte I, p. 32
Considere que as temperaturas de bulbo seco e a de bulbo úmido em um dado ambiente valem 25°C e 21°C, respectivamente. Obtenha a umidade relativa do ar neste ambiente.
Passo 1
A carta psicrométrica funciona da seguinte maneira. Embaixo temos a temperatura de bulbo seco, à direita a pressão de vapor e na diagonal à esquerda temos a entalpia específica do ar úmido e acompanhando essa diagonal porém mais para a direita temos a temperatura de bulbo úmido e finalmente as curvas são curvas de umidade relativa.
Passo 2
Agora temos que achar no gráfico o ponto de interseção entre uma temperatura de bulbo seco de 25°C e úmido de 21°C.
Observe que a curva de umidade relativa que passa nesse ponto é a de valor 70%, logo a umidade relativa desse ambiente é igual a 70%.
Resposta
Exercício Resolvido #5
Elaboração própria
Um estudante de termodinâmica vê no jornal que a umidade relativa está em 50%. Curioso esse estudante vai até o seu termômetro e marca uma temperatura de 30°C, assim ele decide testar seus conhecimentos em psicrometria achando os valores da entalpia específica do ar úmido, umidade absoluta e temperatura de bulbo úmido. Consideranto que ele é um bom aluno e que acertou os valores, quais os valores encontrados pelo aluno?
Passo 1
O primeiro passo é marcar corretamento o ponto em que estamos trabalhando. Seguindo o enunciado vamos estar na interseção da curva de 50% com a vertical de 30°C (temperatura de bulbo seco).
Passo 2
Agora traçamos uma horizontal para a direita para achar a umidade absoluta e uma reta inclinada para cima e para a esquerda para achar tanto a entalpia quanto a temperatura de bulbo úmido.
Assim, a umidade relativa é igual a 0,0135 kg de água / kg de ar seco.
Pode existir um pouco de confusão entre a temperatura de bulbo úmido e a entalpia, porque são parte da mesma reta. Mas é importante lembrar que a entalpia é a mais externa (com menores espaçamentos, e direcionados para fora do gráfico) enquanto a temperatura de bulbo úmido a mais interna (com espaçamentos mais largos e direcionados para dentro do gráfico).
Entalpia será igual a 64 kJ / kg de ar seco.
Temperatura de bulbo úmido será igual a 22°C
Resposta
A umidade relativa é igual a 0,0135 kg de água / kg de ar seco.
Entalpia será igual a 64 kJ / kg de ar seco.
Temperatura de bulbo úmido será igual a 22°C
Exercício Resolvido #6
Elaboração própria
Qual estado possui a menor temperatura de bulbo úmido, o estado com umidade relativa de 80% e temperatura de bulbo seco de 25°C ou o estado com umidade relativa de 100% e temperatura de bulbo seco de 20°C?
Passo 1
Vamos marcar os dois pontos na carta:
Repara que no caso de umidade relativa igual a 100% nem é necessário traçar a reta para achar a temperatura de bulbo úmido (pois como estamos no estado de saturação ambas as temperaturas são iguais).
No caso de 80% de umidade relativa a reta traçada será ligeiramente maior (veja como está acima de 20°C) sendo igual a mais ou menos 22°C.
Resposta
O estado apresenta uma temperatura de bulbo úmido ligeiramente menor.
Exercício Resolvido #7
UNICAMP, Introdução à psicrometria parte I, p. 33 (adaptada)
Considere que as temperaturas de bulbo seco e a de bulbo úmido em um dado ambiente valem 30°C e 20°C, respectivamente. Obtenha a umidade relativa do ar neste ambiente, a umidade absoluta e a entalpia da mistura.
Passo 1
A carta psicrométrica funciona da seguinte maneira. Embaixo temos a temperatura de bulbo seco, à direita a pressão de vapor e na diagonal à esquerda temos a entalpia específica do ar úmido e acompanhando essa diagonal porém mais para a direita temos a temperatura de bulbo úmido e finalmente as curvas são curvas de umidade relativa.
Passo 2
Agora temos que achar no gráfico o ponto de interseção entre uma temperatura de bulbo seco de 30°C e úmido de 20°C.
Temos que a umidade relativa é de 40%, a umidade absoluta é igual a e a entalpia é igual a .
Resposta
Exercício Resolvido #8
UNICAMP, Introdução à psicrometria parte II, p. 14
Ar a 5°C e 70% de umidade relativa é aquecido até 25°C (obs: temperaturas de bulbo seco). A vazão volumétrica é de 50 m3/min (no estado inicial) e a pressão da mistura é P = 100 kPa. Dados: Pressão de saturação a 5°C = 0,872 kPa;
Encontre:
a) A transferência de calor que ocorre durante este processo.
b) A umidade relativa final
Passo 1
A transferência de calor nesse caso (de processo isobárico) é dada por
Então precisamos achar a entalpia dos dois estados (dada pela carta psicrométrica) e a vazão mássica de ar que será encontrada pela equação dos gases na forma
Passo 2
Vamos achar a vazão mássica como mostramos na etapa anterior.
A pressão do ar seco é igual a pressão total menos a pressão do vapor
A pressão do vapor é igual a umidade relativa vezes a pressão de saturação na mesma temperatura
Substituindo os valores encontrados para achar a massa específica
Agora podemos achar a vazão mássica
Passo 3
Neste passo iremos achar as entalpias dos estados 1 e 2. Para isso vamos utilizar a carta psicrométrica. Para o estado 1 temos uma entalpia de e umidade absoluta de aproximadamente .
Para o estado 2 vamos ter uma entalpia de e uma umidade relativa de 20%.
Observe que com duas informações é possível achar um ponto específico na carta e com isso achar os outros valores importantes. No primeiro caso utilizamos a umidade relativa e a temperatura, já no segundo utilizamos a temperatura e a umidade absoluta (que foi retirada do primeiro caso, já que não houve aumento em massa da quantidade de água).
Passo 4
Logo a quantidade de calor é igual a