Composição dos Combustíveis
Produzido por Philip Canabarro BlockerTeoria
Mistura de combustíveis
Até agora, nós só aprendemos a calcular os coeficientes estequiométricos de um único tipo de combustão. Só estudamos as reações de combustíveis que têm apenas um componente. Por exemplo, estudamos a combustão do metano . Ele é um combustível que possui só um tipo de molécula: o ! Ele não é formado por uma mistura de moléculas diferentes!
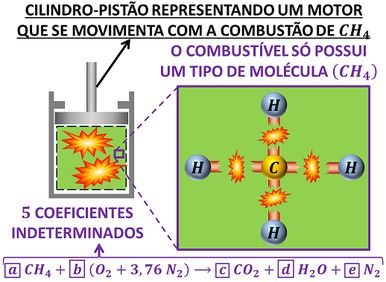
Começar os estudos por combustíveis mais simples, facilitou o nosso aprendizado, quando a gente ainda estava descobrindo o que era um balanço químico. No entanto, na vida real e nas questões de prova o problema é um pouco mais complicado. Geralmente, os combustíveis usados em máquinas reais são formados por uma mistura de vários tipos de moléculas!
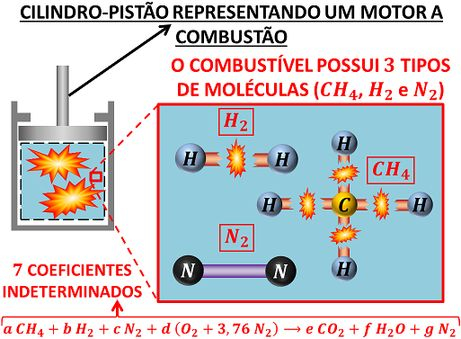
Como podemos calcular os coeficientes estequiométricos de reações de combustíveis misturados? Será que temos equações o suficiente para calcular os coeficientes a mais desses combustíveis?
Composição dos combustíveis gasosos em base volumétrica ou base molar
Relaxa, porque todo exercício tem solução! Nós conseguimos calcular os coeficientes, porque o enunciado dessas questões mais complicadas informa a composição do combustível misturado! Vamos entender como usar esse dado a mais com um exemplo!

Determine os coeficientes estequiométricos da reação de um combustível gasoso com ar seco. Considere que essa combustão só forma gás carbônico , água e gás nitrogênio . A composição desse combustível está mostrada na tabela abaixo em base volumétrica.
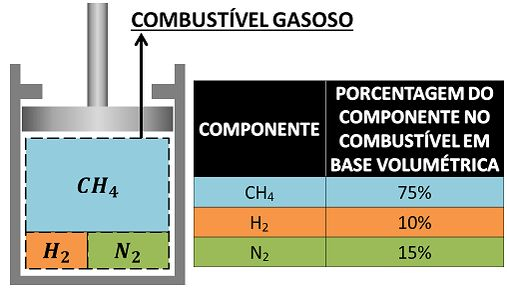
Primeiro de tudo: o que seria essa base volumétrica? Saber isso é fundamental para resolver esse tipo de questão! A base volumétrica é igual à base molar! Isso quer dizer que todas as porcentagens mostradas na tabela são a fração molar de cada componente.
A base volumétrica é usada para mostrar a composição de combustíveis é gasosos!
onde:
- é a quantidade de de dentro do combustível;
- é a quantidade de de dentro do combustível;
- é a quantidade de de dentro do combustível;
- é a quantidade de do combustível. Ele é a soma do de cada componente.
Agora vamos traduzir o que todas essas variáveis e números significam! Quando a tabela informa que de combustível é composto por , ela quer dizer que em cada de combustível existem de . Isso também serve pros outros componentes. Em cada de combustível existem de e de .
Cálculo dos coeficientes estequiométricos do combustível gasoso misturado
Acabamos de descobrir o que significam as porcentagens da tabela. Mas como podemos calcular os coeficientes estequiométricos do combustível misturado, usando essa informação?
Para fazer isso, podemos escrever a equação química de combustão para de combustível. Com isso, descobrimos a quantidade de de cada componente.
Os coeficientes restantes são determinados pelo balanço de cada elemento químico. Em outras palavras, os números que faltam são encontrados, quando a gente iguala a quantidade de um elemento presente nos reagentes com a quantidade desse elemento presente nos produtos.
Com esses valores a equação química fica:
Mas, por que a gente escolheu escrever a equação química para de combustível?
Porque a equação química é que nem uma receita de bolo. O que importa de verdade nela é a proporção entre as substâncias. Se a gente escrevesse a equação para de combustível, a proporção entre o e o continuaria sendo de pra ( ou ). Isso que importa!
Composição dos combustíveis líquidos e sólidos em base mássica
Foi dito que a composição dos combustíveis gasosos era mostrada em base volumétrica ou base molar. Isso quer dizer que a composição de combustíveis líquidos (gasolina, óleo diesel e etanol) e sólidos (carvão) é mostrada em uma base diferente? Sim! Em exercícios de termodinâmica, a composição desses dois tipos de combustível é mostrada em base mássica!

Isso muda um pouco a forma como calculamos os coeficientes estequiométricos de cada substância! Para fazer essa conta, a gente vai precisar saber a massa molar de cada componente do combustível. Mas não se preocupe! Se o próprio enunciado não informar as massas molares, você terá acesso a esses valores em tabelas! A figura abaixo é um exemplo.
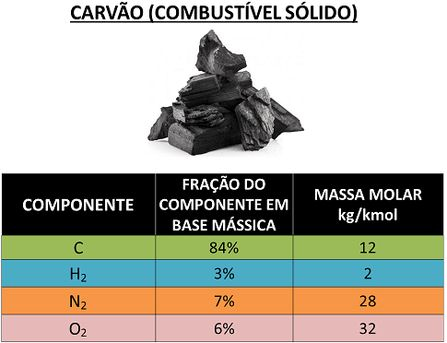
Determine os coeficientes estequiométricos da combustão do carvão com ar seco. Considere que essa combustão só forma gás carbônico , água e gás nitrogênio . A composição do carvão está mostrada na tabela acima em base mássica.
Podemos escrever a equação química da combustão com os coeficientes desconhecidos.
Mas por onde podemos iniciar os cálculos?
Veremos isso no próximo tópico!
O que são as porcentagens de uma composição em base mássica?
O primeiro passo para resolver esse exemplo é entender direitinho o que é base mássica. Quando a composição é mostrada em base molar, as porcentagens são o do componente dividido pelo total do combustível. Quando a composição está em base mássica, as porcentagens são a massa do componente dividido pela massa do combustível.
onde é a massa em quilograma . Por exemplo, é a massa de em quilograma presente combustível. é a massa de todo o combustível em quilograma . Por isso, ela é a soma da massa de cada componente.
é a concentração da substância. Por exemplo, é a concentração de no carvão. também pode ser chamada de fração mássica. Por conta disso, é chamada de fração mássica de no combustível.

Mas como podemos calcular os coeficientes estequiométricos do carvão, usando essas porcentagens?
Para fazer isso, podemos escrever a equação química de combustão do carvão para de combustível. Com isso, descobrimos a quantidade de de cada componente.
A partir desses valores de massa, nós vamos calcular a quantidade de de cada substância, dividindo a massa da substância pela sua massa molar !
Cálculo dos coeficientes estequiométricos de um combustível em base mássica
Com isso, descobrimos a quantidade de de cada componente.
Os coeficientes restantes são determinados pelo balanço de cada elemento químico.
Com esses valores a equação química fica:
O mesmo comentário feito antes para composição em base volumétrica pode ser feito para composição em base mássica! A gente escolheu escrever a equação química para de combustível, mas poderia escolher qualquer outro valor de massa do combustível. Isso não vai mudar a proporção entre as substâncias e é só essa proporção que importa na equação!
Cálculo dos coeficientes estequiométricos do combustível gasoso misturado
Composição dos combustíveis líquidos e sólidos em base mássica
O que são as porcentagens de uma composição em base mássica?
Cálculo dos coeficientes estequiométricos de um combustível em base mássica
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
de uma mistura de gás natural com uma análise molar de de e de é queimada completamente com ar seco. Essa queima gera gás carbônico , vapor d’água e nitrogênio . Determine as massas de gás carbônico e vapor d’água produzidas por essa combustão.
Passo 1
Oi, gente, tudo bem? Bora partir direto para o que nos interessa?

O enunciado quer que a gente encontre o valor da massa de e da massa de . Pra isso, temos, primeiro, que escrever a equação química da reação de combustão do enunciado. O enunciado diz que de e de reagem com de e de , formando de , de e de .
Para acharmos e , precisamos encontrar e . e , são determinados através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de de e a quantidade de de presentes dentro dos da mistura combustível. Calculamos , multiplicando os de combustível pela porcentagem molar de que existe no combustível.
Achamos a quantidade de de no combustível, usano o mesmo método: multiplicamos os da mistura pelos de que existem nela!
Substituindo essas informações na equação química de combustão, encontramos a seguinte reação.
Com essa equação química já somos capazes de achar e e partir pro cálculo de e !
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes em mais de presentes no dos reagentes.
Para achar , precisamos fazer o balanço de hidrogênio . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes em nos reagentes.
Pra achar , temos que multiplicar o valor da massa molar da água pela quantidade de de produzida pela combustão. Logo:
Pra achar , usamos o mesmo método. Multiplicamos a massa molar de pela quantidade de de .
Uhuuuul achamos as massas que o enunciado pediu! Mandamos muito!
Resposta
Exercício Resolvido #2
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise elementar (base mássica): de carbono , de oxigênio e de cinzas.
Admitindo que a amostra deste carvão é queimada com ar seco, formando gás carbônico e nitrogênio , calcule a fração mássica de e nos produtos.
Passo 1
E aí, querid@s! Vamos fazer um exercício de combustão de combustíveis misturados pra alegrar seu dia?

O enunciado quer que a gente encontre o valor da fração mássica de e da fração mássica de nos produtos. é a massa de dividida pela massa total dos produtos . é a massa de dividida pela massa total dos produtos .
Pra achar as massas , e , temos, primeiro, que escrever a equação química da reação de combustão do enunciado. O enunciado diz que de e de reagem com de do ar e de do ar, formando de e de . Atenção! As cinzas não entram na equação química. Por isso são desprezadas!
Para acharmos , e , precisamos encontrar e . e são determinados através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de de e a quantidade de de presentes dentro da mistura combustível. Calculamos , supondo que de combustível são queimados. Achamos a massa de multiplicando os pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando os pelos de no combustível.
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Além disso, precisamos lembrar que, a cada de presente no ar, existem de presentes no ar. Ou seja, a quantidade de do é maior que a quantidade de do !
Substituindo essas informações na equação química de combustão, encontramos a seguinte reação.
Com essa equação química já somos capazes de achar e e partir pro cálculo de e !
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes.
Para achar , precisamos achar primeiro. Achamos , fazendo o balanço de oxigênio . Para a quantidade de ficar balanceada, os de dos produtos têm que ser iguais aos de presentes no do combustível mais os de do ar.
Enfim, achamos fazendo o balanço de nitrogênio . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes.
Conhecendo essa equação química, somos capazes de achar as frações mássicas no próximo passo!
Passo 4
Pra achar , temos que multiplicar o valor da massa molar do nitrogênio pela quantidade de de produzida pela combustão. Logo:
Pra achar , usamos o mesmo método. Multiplicamos a massa molar de pela quantidade de de .
Como e são os produtos da combustão, a massa total dos produtos é a soma das massas de e .
Substituindo as massas nas fórmulas de e :
Boaaaaaa! Achamos as duas frações mássicas! Arrasamos!
Resposta
Exercício Resolvido #3
Elaboração própria
Uma mistura gasosa com a análise molar de , de , de e de reagem com ar seco para gerar produtos que consistem apenas de , e . Determine a análise molar dos produtos secos.
Passo 1
Oier, querid@s! Bora direto ao ponto pra entender logo o que a questão quer e resolver tudo?
O enunciado quer que a gente encontre o valor de frações molares dos produtos sem considerar o : a fração de e a fração de .
é a quantidade de de dividida pela quantidade de dos produtos .
Da mesma forma, é a quantidade de de dividida pela quantidade de dos produtos .
Pra achar , e , temos, primeiro, que escrever a equação química da reação de combustão do enunciado. O enunciado diz que de , de , de e de reagem com ar seco ( de e de ), formando de , de e de .
Para acharmos , e precisamos encontrar , , , e . , , , e são determinados através do balanço da equação química vista no próximo passo!
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de dos componentes que formam o combustível. Ou seja, temos que achar de de , a quantidade de de e a quantidade de de presentes dentro da mistura combustível.

Calculamos , supondo que de combustível é queimado. Podemos supor que qualquer quantidade de de combustível é queimada, porque isso não interfere no cálculo das frações molares! Achamos a quantidade de de , multiplicando pelos de no combustível.
Da mesma forma, achamos a quantidade de de , multiplicando os pelos de no combustível. A quantidade de de é encontrada, multiplicando os pelos de no combustível! Por fim, calculamos a quantidade de de , multiplicando do combustível pelos de .
Substituindo essas informações na equação química de combustão, encontramos a seguinte reação.
Com essa equação química já somos capazes de achar , , e e partir pro cálculo de e !
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes em mais de presente em .
Para achar , precisamos achar e primeiro. Achamos , fazendo o balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos produtos têm que ser iguais aos de dos reagentes.
Para a quantidade de ficar balanceada e encontrarmos , os de presentes no mais de presente no têm que ser iguais aos de presentes no do combustível, mais de presente no , mais de presente no do ar .
Por fim, achamos , balanceando a quantidade de nitrogênio . Pra isso, os de do do combustível mais os de do do ar devem ser iguais aos de dos produtos.
Pronto! Agora sim somos capazes de achar as frações molares no próximo passo!
Passo 4
Como e são os únicos produtos da combustão além de , a quantidade total de dos produtos , excluindo o (porque o enunciado quer saber sobre os produtos secos) é a soma das quantidades de de e .
Substituindo as massas nas fórmulas de e :
Uhuuuuul! Achamos as frações molares e chegamos no fim do exercício!
Resposta
Exercício Resolvido #4
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 703-13.10
Uma mistura gasosa com a análise molar de , de , de reage para gerar produtos que consistem apenas de , e . Determine a quantidade de cada produto, em por da mistura.
Passo 1
Oi, fof@s! Vamos direto ao ponto pra entender logo o que a questão quer?
O enunciado quer que a gente encontre o valor de frações mássicas dos produtos: a fração de , a fração de e a fração de . é a massa de dividida pela massa total dos produtos .
Da mesma forma, é a massa de dividida pela massa total dos produtos . Por fim, temos que é a massa de dividida pela massa total dos produtos .
Pra achar as massas , , e , temos, primeiro, que escrever a equação química da reação de combustão do enunciado. O enunciado diz que de e de reagem com de do combustível, formando de , de e de . Atenção! As cinzas não entram na equação química. Por isso são desprezadas!
É importante notar que, como não tem nitrogênio nos produtos, podemos assumir a reação de combustão foi realizada com o oxigênio do combustível e não com a mistura de com do ar! Para acharmos , , e precisamos encontrar , e . , e são determinados através do balanço da equação química vista no próximo passo!
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de de , a quantidade de de e a quantidade de de presentes dentro da mistura combustível.

Calculamos , supondo que de combustível é queimado. Podemos supor que qualquer quantidade de de combustível é queimada, porque isso não interfere no cálculo das frações mássicas! Achamos a quantidade de de , multiplicando pelos de no combustível.
Da mesma forma, achamos a quantidade de de , multiplicando os pelos de no combustível e calculamos a quantidade de de , multiplicando os pelos de no combustível!
Substituindo essas informações na equação química de combustão, encontramos a seguinte reação.
Com essa equação química já somos capazes de achar , e e partir pro cálculo de , e !
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes.
Para achar , precisamos achar primeiro. Achamos , fazendo o balanço de hidrogênio .
Para a quantidade de ficar balanceada, os de dos produtos têm que ser iguais aos de dos reagentes.
Para a quantidade de ficar balanceada e encontrarmos , os de presente no mais de presente no mais de presente no têm que ser iguais aos de presentes no do combustível, mais de presente no .
Conhecendo essa equação química, somos capazes de achar as frações mássicas no próximo passo!
Passo 4
Pra achar , temos que multiplicar o valor da massa molar do oxigênio por de produzido pela combustão. Logo:
Achamos , usando o mesmo método. Multiplicamos a massa molar de por de .
Por fim, pra achar , temos que multiplicar o valor da massa molar da água por de .
Como , e são os produtos da combustão, a massa total dos produtos é a soma das massas de , e .
Substituindo as massas nas fórmulas de , e :
Chegamos no fim do exercício com os resultados que o enunciado nos pediu!
Resposta
Exercício Resolvido #5
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e o restante de cinzas não combustíveis.
Admitindo que a amostra deste carvão é queimada com ar seco, formando gás carbônico , nitrogênio , vapor d’água e dióxido e enxofre , determine a análise molar dos produtos.
Passo 1
Faaala, galera! Esse enunciado é cheio de informação, né? Ele fala sobre uma reação de combustão que envolve tantas moléculas que fica difícil entender quais são os reagentes e os produtos. Por isso, nosso primeiro passo deve ser escrever a equação química da combustão, mostrando os reagentes e produtos sem os valores dos coeficientes estequiométricos.

O enuciado diz que , , , e reagem com ar seco que é composto por uma parte de e partes de . Como essas moléculas reagem, elas são os reagentes, certo?
O enunciado também diz que , , e são produzidos pela reação. Logo, essas moléculas são os produtos. Colocando os reagentes na esquerda e produtos na direita:
, , , , , , , , e são os coeficientes estequiométricos da equação química!
As cinzas não estão nessa equação, porque não participam da reação!
Esses coeficientes estequiométricos precisam ser encontrados para encontrarmos as frações molares que o enunciado pede: , , e . As fórmulas das frações estão abaixo.
onde é a quantidade de total dos produtos! Ou seja, é a soma entre , , e . Esses coeficientes dos produtos são determinados através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de (no nosso caso , , , e ) dos componentes do combustível. Calcularemos , supondo que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontarda, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Nós calculamos as massas pro caso de de combustível serem queimados, mas essa quantidade de combustível não interfere no cálculo das frações molares!
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes. A equação química é mostrada abaixo pra enxergarmos melhor.
Da mesma forma, achamos , fazendo o balanço do hidrogênio . Os do produto têm que ser iguais aos do reagente.
também pode ser encontrado logo, fazendo o balanço do enxofre . Para a quantidade de ficar balanceada, os de dos produtos devem ser iguais aos de dos reagentes.
Agora podemos achar o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Com esses coeficientes em mãos, podemos finalmente calcular o coeficiente através do balanço de . Os de dos reagentes têm que ser iguais aos de dos produtos!
Agora sim estamos aptos a calcular frações molares no próximo passo!
Passo 4
Como , , e são os produtos da combustão, a quantidade total de dos produtos é a soma das quantidades de de , , e .
Substituindo as quantidades de nas fórmulas de , , e :
Boaaaaaa! Achamos todas as frações molares! Mandamos muito bem!
Resposta
Exercício Resolvido #6
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e o restante de cinzas não combustíveis.
Admitindo que a amostra deste carvão é queimada com ar seco, formando gás carbônico , nitrogênio , vapor d’água e dióxido e enxofre , determine a razão entre a massa de ar e a massa de combustível necessária para essa reação ocorrer.
Passo 1
Oie, galera! Esse enunciado é cheio de informação, né? Ele fala sobre uma reação de combustão que envolve tantas moléculas que fica difícil entender quais são os reagentes e produtos. Por isso, nosso primeiro passo deve ser escrever a equação química da combustão, mostrando os reagentes e produtos sem os valores dos coeficientes estequiométricos.

O enuciado diz que , , , e reagem com ar seco que é composto por uma parte de e partes de . Como essas moléculas reagem, elas são os reagentes, certo?
O enunciado também diz que , , e são produzidos pela reação. Logo, essas moléculas são os produtos. Colocando os reagentes na esquerda e produtos na direita:
, , , , , , , , e são os coeficientes estequiométricos da equação química!
As cinzas não estão nessa equação, porque não participam da reação!
Esses coeficientes estequiométricos precisam ser encontrados para encontrarmos a razão entre a massa de ar e a massa de combustível.
Essas massas são determinadas através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de (no nosso caso , , , e ) dos componentes do combustível. Calcularemos , supondo que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontrada, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Nós calculamos as massas pro caso de de combustível serem queimados, mas poderia ser qualquer quantidade de combustível! Esse valor não interfere no cálculo de !
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes. A equação química é mostrada abaixo pra enxergarmos melhor.
Da mesma forma, achamos , fazendo o balanço do hidrogênio . Os do produto têm que ser iguais aos do reagente.
também pode ser encontrado logo, fazendo o balanço do enxofre . Para a quantidade de ficar balanceada, os de dos produtos devem ser iguais aos de dos reagentes.
Agora podemos achar o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Agora sim estamos aptos a calcular a razão entre a massa de ar e a massa de combustível no próximo passo!
Passo 4
Como o ar seco é composto de e , a massa do ar seco é a soma entre a massa de nitrogênio presente no ar e a massa de oxigênio presente no ar.
Pra achar , temos que multiplicar o valor da massa molar do nitrogênio por de do ar. Logo:
Achamos , usando o mesmo método. Multiplicamos a massa molar de por de .
Substituindo as duas massas na fórmula de :
A massa de combustível vale , porque assumimos que foram queimados de combustível para fazer o balanço da equação.
Com e somos capazes de achar !
Que coisa boa! Já chegamos ao final desse exercício! Tudo que é bom passa rápido, né?
Resposta
Exercício Resolvido #7
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e o restante de cinzas não combustíveis.
Admitindo que a amostra deste carvão é queimada com ar seco, formando gás carbônico , nitrogênio , vapor d’água e dióxido e enxofre , determine a análise mássica dos produtos.
Passo 1
Oooi, pessoal! Esse enunciado é cheio de informação, né? Ele fala sobre uma reação de combustão que envolve tantas moléculas que fica difícil entender quais são os reagentes e os produtos. Por isso, nosso primeiro passo deve ser escrever a equação química da combustão, mostrando os reagentes e produtos sem os valores dos coeficientes estequiométricos..

O enuciado diz que , , , e reagem com ar seco que é composto por uma parte de e partes de . Como essas moléculas reagem, elas são os reagentes, certo?
O enunciado também diz que , , e são produzidos pela reação. Logo, essas moléculas são os produtos. Colocando os reagentes na esquerda e produtos na direita:
, , , , , , , , e são os coeficientes estequiométricos da equação química!
As cinzas não estão nessa equação, porque não participam da reação!
Esses coeficientes estequiométricos precisam ser encontrados para encontrarmos as frações mássicas que o enunciado pede: , , e . As fórmulas das frações estão abaixo.
onde é a massa total dos produtos! Ou seja, é a soma entre , , e . Essas massas dos produtos são determinadas através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de (no nosso caso , , , e ) dos componentes do combustível. Calcularemos , supondo que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontarda, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Nós calculamos as massas pro caso de de combustível serem queimados, mas essa quantidade de combustível não interfere no cálculo das frações mássicas!
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes. A equação química é mostrada abaixo pra enxergarmos melhor.
Da mesma forma, achamos , fazendo o balanço do hidrogênio . Os do produto têm que ser iguais aos do reagente.
também pode ser encontrado logo, fazendo o balanço do enxofre . Para a quantidade de ficar balanceada, os de dos produtos devem ser iguais aos de dos reagentes.
Agora podemos achar o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Com esses coeficientes em mãos, podemos finalmente calcular o coeficiente através do balanço de . Os de dos reagentes têm que ser iguais aos de dos produtos!
Agora sim estamos aptos a calcular frações mássicas no próximo passo!
Passo 4
Pra achar , temos que multiplicar o valor da massa molar do nitrogênio por de produzido pela combustão. Logo:
Achamos , usando o mesmo método. Multiplicamos a massa molar de por de .
é calculado do mesmo jeito. Multiplicamos a massa molar de por de .
Por fim, pra achar , temos que multiplicar o valor da massa molar da água por de .
Como , , e são os produtos da combustão, a massa total dos produtos é a soma das massas de , , e . Por isso:
Substituindo as massas nas fórmulas de , , e :
Shoooowww! Calculamos todas as frações mássicas! Pode comemorar!
Resposta
Exercício Resolvido #8
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e de cinzas não combustíveis.
A amostra deste carvão é queimada com ar seco, formando gás carbônico , nitrogênio , vapor d’água e dióxido e enxofre . Considerando que os produtos de combustão se encontram a pressão total de , determine a temperatura do ponto de orvalho dos produtos.
Passo 1
Oooi, pessoal! Esse enunciado é cheio de informação, né? Ele fala sobre uma reação de combustão que envolve tantas moléculas que fica difícil entender quais são os reagentes e os produtos. Por isso, nosso primeiro passo deve ser escrever a equação química da combustão, mostrando os reagentes e produtos sem os valores dos coeficientes estequiométricos..

O enuciado diz que , , , e reagem com ar seco que é composto por uma parte de e partes de . Como essas moléculas reagem, elas são os reagentes, certo?
O enunciado também diz que , , e são produzidos pela reação. Logo, essas moléculas são os produtos. Colocando os reagentes na esquerda e produtos na direita:
, , , , , , , , e são os coeficientes estequiométricos da equação química! As cinzas não estão nessa equação, porque não participam da reação! Esses coeficientes estequiométricos precisam ser encontrados para encontrarmos a temperatura do ponto de orvalho dos produtos. Ela é a temperatura de saturação da água na pressão parcial da água.
onde é a pressão parcial do vapor d’água nos produtos. Essa pressão parcial é igual à pressão total dos produtos multiplicada pela fraçõ molar da água nos produtos.
A fração molar de água é igual à quantidade de de água nos produtos dividida pela quantidade de total dos produtos .
é a soma entre , , e . Esses coeficientes dos produtos são determinados através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de (no nosso caso , , , e ) dos componentes do combustível. Calcularemos , supondo que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontarda, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Nós calculamos as massas pro caso de de combustível serem queimados, mas tanto faz a quantidade de combustível que supomos ser queimada. Ela não interfere no cálculo de !
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes. A equação química é mostrada abaixo pra enxergarmos melhor.
Da mesma forma, achamos , fazendo o balanço do hidrogênio . Os do produto têm que ser iguais aos do reagente.
também pode ser encontrado logo, fazendo o balanço do enxofre . Para a quantidade de ficar balanceada, os de dos produtos devem ser iguais aos de dos reagentes.
Agora podemos achar o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Com esses coeficientes em mãos, podemos finalmente calcular o coeficiente através do balanço de . Os de dos reagentes têm que ser iguais aos de dos produtos!
Agora sim estamos aptos a calcular a fração molar da água pra achar no próximo passo!
Passo 4
Como , , e são os produtos da combustão, a quantidade total de dos produtos é a soma das quantidades de de , , e .
Substituindo essa quantidade de na fórmula de :
Com esse valor, somos capazes de achar a pressão parcial do vapor d’água nos produtos.
A temperatura de ponto de orvalho é a temperatura de saturação da água a . Logo, temos que usar a tabela termodinâmica da água pra achar . Como essa tabela não possui o valor de temperatura de saturação para esse valor de pressão, nós temos que interpolar a temperatura, usando os valores de temperatura de saturação a e .
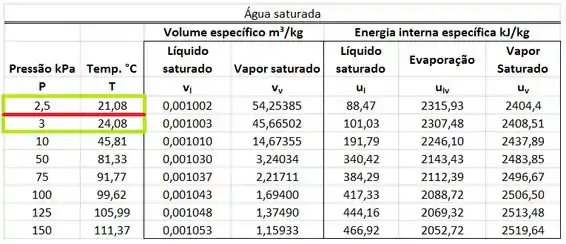
Aeeeee! Achamos o valor da temperatura de ponto de orvalho dos produtos! Ela vale ! Isso quer dizer que se a gente resfriar os produtos gerados pela combustão a pressão constante, quando eles chegarem na temperatura de , a água dos produtos começará a condensar.