Primeira Lei para Combustão
Teoria
A primeira lei para processos sem reação não serve para questões de combustão!
Até agora nós só resolvemos exercícios de primeira lei de processos sem reação química. Quando o processo sem reação química ocorre dentro de um volume de controle, a primeira lei que usamos tem a forma abaixo. Essa é uma forma simplificada da primeira lei, porque ela despreza as variações das energias cinética e potencial.
Essa forma da primeira lei era muito útil para processos sem reação química, porque as tabelas que a gente usava nos davam diretamente os valores das entalpias por unidade de massa presentes na fórmula.
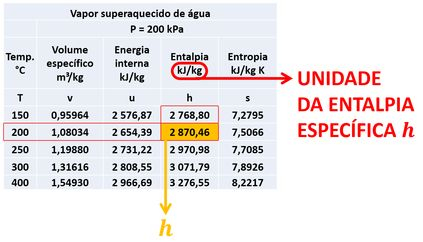
No entanto, as tabelas que usamos para resolver questões com reação química, geralmente, só nos mostram valores de entalpia por . Isso significa que nós só conhecemos os valores de entalpia por , mas as equações que temos só usam valores de por unidade de massa .
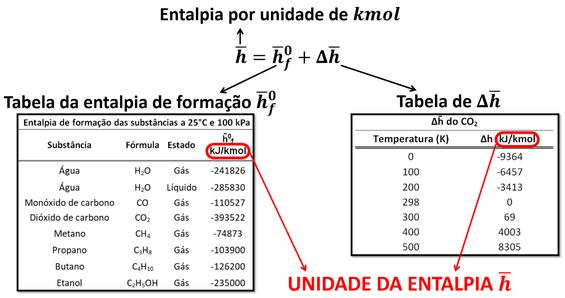
Existe uma forma da primeira lei que usa os valores da entalpia por ?
Primeira lei para combustão em um volume de controle em regime permanente
Essa forma diferentes da primeira lei existe! Além disso, ela é bem parecida com a forma antiga que já conhecemos! A forma da primeira lei usada em questões de combustão em volume de controle em regime permanente é mostrada abaixo. Essa fórmula considera que as variações de energia potencial e energia cinética são desprezíveis.
Para transformar a primeira lei antiga na primeira lei nova, nós só mudamos dois termos: e . Nós trocamos as entalpias por unidade de massa multiplicadas pelas vazões mássicas pelas entalpias por multiplicadas pela vazões molares .
Os significados de e não mudam! é a taxa de calor trocado entre o volume de controle e o ambiente. é a taxa de trabalho (também chamada de potência) realizada pelo volume de controle sobre o ambiente. A unidade de e no Sistema Internacional de Unidades (S.I.) é o watt . Os outros termos dessa fórmula são mostrados na figura abaixo.
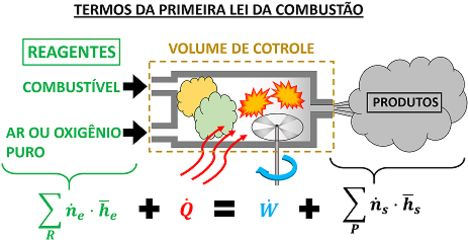
é a vazão molar do reagente da combustão, entrando no volume de controle. é a vazão molar do produto da combustão, saindo do volume de controle. Assim como a vazão mássica é a quantidade de massa que passa pelo volume de controle, a vazão molar é a quantidade de quilomol que passa pelo volume de controle.
A unidade de e no Sistema Internacional de Unidades (S.I.) é o quilomol por segundo .
é a entalpia específica em base molar do reagente da combustão e é a entalpia específica em base molar do produto da combustão. A unidade de e no Sistema Internacional de Unidades (S.I.) é o quilojoule por quilomol . Para calcular essas entalpias , precisamos usar a fórmula abaixo.
onde:
- é a entalpia de formação da substância e . Ela está em base molar. Sua unidade no Sistema Internacional (S.I.) é o quilojoule por quilomol ;
- é a diferença entre a entalpia específica da substância a uma temperatura qualquer e a uma pressão qualquer e a entalpia específica da substância a e . Ela está em base molar e seu valor é encontrado em tabelas. Sua unidade no Sistema Internacional (S.I.) é o quilojoule por quilomol .
Substituindo essa fórmula na primeira lei, ela vira:
Essa é a fórmula que nós usaremos para resolver as questões de volume de controle! Então vamos resolver um exemplo para aprender a usar essa equação.
Como usar a primeira lei para combustão em regime permanente
Gás metano e oxigênio puro entram em uma câmara de combustão a e a para reagir em regime permanente. Os produtos da combustão também estão a e a . Considerando que a combustão é completa e que ela gera água líquida, determine a quantidade de calor liberada durante a reação por de .
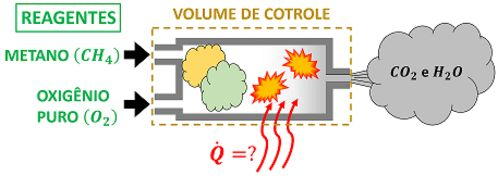
O exemplo quer saber o valor de . Ele nos deu a temperatura e a pressão dos produtos e reagentes para a gente conseguir calcular os valores de entalpia por . O enunciado não falou nada sobre a realização de trabalho do volume de controle. No entanto, os exercícios de primeira lei da combustão não costumam envolver trabalho. Por isso:
A primeira etapa para calcular por de um combustível é escrever a equação química da sua combustão para de combustível Temos que lembrar também que na combustão completa do só são formados o e o .
Note que os coeficientes estequiométricos , e ainda não foram determinados. O valor deles pode ser calculado a partir do balanço de cada elemento químico da equação (, e ).
Agora sim podemos usar a primeira lei. Precisamos reorganizar a equação para criar uma fórmula de por de .
Existem dois somatórios nessa fórmula. O somatório dos reagentes que entram no volume de controle e o somatório dos produtos que saem do volume de controle . Os reagentes da combustão do metano são o metano e o oxigênio . Os produtos da combustão são o gás carbônico e a água líquida .
As vazões molares , , e são determinadas na segunda etapa de cálculo de por de !
Segunda etapa de cálculo do calor liberado por de combustível
As vazões molares são iguais aos coeficientes estequiométricos das substâncias. Por exemplo, o coeficiente estequiométrico do metano vale . Por isso:
Seguem abaixo os valores das vazões molares que restam. Eles foram calculados com o mesmo raciocínio usado para a vazão molar do metano .
Cada entalpia é a soma de duas partes. A primeira parte é a entalpia de formação da substância e a segunda parte é a diferença entre a entalpia da substância na temperatura e na pressão em que ela se encontra e a entalpia da substância a temperatura e a pressão . Os valores de e estão em tabelas.
Como todos os produtos e reagentes da combustão estão a e a , a diferença vale zero para todos eles.
Precisamos tomar cuidado com a entalpia da água . O caso da água é especial, porque as tabelas de entalpia de formação mostram dois valores diferentes para entalpia de formação da água. Um para água no estado de vapor ou gás e outro para a água no estado de líquido .
No nosso caso, usaremos a entalpia de formação da água líquida, porque o enunciado nos diz que a água presente nos produtos da combustão é líquida! Com isso, a entalpia da água pode ser calculada.
Última etapa de cálculo do calor liberado por de combustível
Nessa última etapa nós substituímos os valores de entalpia que encontramos na fórmula que criamos para por de combustível!
Isso significa que a cada de queimado com oxigênio puro , a reação libera calor a uma taxa de . Em outras palavras de calor saem da câmara de combustão a cada segundo que de é queimado.
Como usar a primeira lei para combustão em regime permanente
Segunda etapa de cálculo do calor liberado por k m o l de combustível
Última etapa de cálculo do calor liberado por k m o l de combustível
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Uma câmara de combustão operando em regime permanente descarrega de produtos. A análise volumétrica desse produto mostra que ele é composto de , de e de . A água se encontra em estado líquido. Considerando que esse produto de combustão se encontra a e a pressão atmosférica, determine a energia contida nele.
Passo 1
Então, pessoal, esse é um exercício de combustão que pede pra gente calcular a energia dos produtos de uma combustão! Como a combustão ocorre em regime permanente, essa energia é igual à soma das entalpias de , e que compõe o produto. A soma é mostrada na fórmula abaixo!
, e são as vazões molares de , e . são as entalpias de formação dos componentes do produto e é a diferença entre a entalpia da substância e a entalpia que a substância teria caso estivesse a .
Começamos os cálculos, determinando as vazões molares de , e !
Passo 2
O enunciado disse que o produto é composto por . Como a vazão molar total do produto é de , a vazão de é disso!
O mesmo vale pro e pro . A vazão de é de e a vazão de é de .
Pronto! Achamos as vazões molares. Agora falta achar as entalpias de formação e as diferenças de entalpia pra calcular .
Passo 3
As entalpias de formação de vale zero, porque é uma substância quimicamente mais estável.
A entalpia de formação de e de líquido é encontrada em tabelas, como a tabela abaixo.
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia . No entanto, é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os produtos e reagentes estão a , vale zero pra todas as substâncias.
Com esses valores podemos achar na próxima etapa!
Passo 4
Substituindo os valores que temos, achamos:
Colocando estes valores na fórmula de :
Shooooow! Terminamos com a questão!
Resposta
Exercício Resolvido #2
Elaboração própria
Carvão composto totalmente por carbono é queimado, à pressão atmosférica, com quantidade estequiométrica de ar. Calcule o calor rejeitado, em de combustível, sabendo que os produtos e reagentes estão a .
Passo 1
Então, pessoal, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível dividida pela quantidade de combustível queimada a cada segundo .
Para achar essa quantidade, temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é rejeitado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Começamos a calcular as vazões molares, escrevendo a equação química da combustão. O enunciado diz que a combustão é completa sem excesso de ar (quantidade estequiométrica de ar). Isso significa que apenas e são os produtos. Como o ar é composto por e , o , o e o são os reagentes.
onde , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar do combustível .
Como a questão está interessada na taxa de calor liberada por cada de combustível, vamos calcular o calor, quando a quantidade de de queimado vale .
Para achar os outros coeficientes, temos que fazer o balanço da equação de reação.
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de é igual à , a vazão molar de dos reagentes e dos produtos é igual a e a vazão molar de é igual à .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 3
As entalpias de formação de, , e valem zero porque os três são substâncias quimicamente mais estáveis.
A entalpia de formação de é encontrada em tabelas, como a tabela abaixo.
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia . No entanto, é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os produtos e reagentes estão a , vale zero pra todas as substâncias.
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 4
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Dividindo pela vazão de combustível :
Show de bola! Acabamos com a questão! Agora pode relaxar! Você conseguiu entender a matéria!
Resposta
Exercício Resolvido #3
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 803-15.49
Etano é queimado, à pressão atmosférica, com quantidade estequiométrica de ar como oxidante. Determine o calor rejeitado, em de combustível, considerando que os produtos e reagentes estão a e a água aparece nos produtos como vapor de água.
Passo 1
Então, galera, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível dividida pela quantidade de combustível queimada a cada segundo .
Para achar essa quantidade, temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é rejeitado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Começamos a calcular as vazões molares, escrevendo a equação química da combustão. O enunciado diz que a combustão é completa sem excesso de ar (quantidade estequiométrica de ar). Isso significa que apenas , e são os produtos. Como o ar é composto por e , o , o e o são os reagentes.
onde , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar do combustível .
Como a questão está interessada na taxa de calor liberada por cada de combustível, vamos calcular o calor, quando a quantidade de de queimado vale .
Para achar os outros coeficientes, temos que fazer o balanço da equação de reação.
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à e a vazão molar de é igual à .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 3
As entalpias de formação do e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! Precisamos pegar o valor da entalpia de formação de vapor de !
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia . No entanto, é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os produtos e reagentes estão a , vale zero pra todas as substâncias.
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 4
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Dividindo pela vazão de combustível :
Chegamos na resposta! Agoooora sim pode sorrir e comemorar essa vitória com a família!
Resposta
Exercício Resolvido #4
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 804-15.60
O metano é completamente queimado com a quantidade estequiométrica de ar durante um processo de combustão em regime permanente. Considerando que os reagentes e os produtos são mantidos a e e que a água dos produtos existe na forma líquida, determine a quantidade de calor transferida da câmara de combustão durante esse processo. Qual seria sua resposta caso a combustão fosse realizada com de excesso de ar?
Passo 1
Gente, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível em duas situações diferentes. Na primeira situação, o exercício pede pra gente calcular a taxa de calor liberada na combustão completa de sem excesso de ar dividida pela quantidade de de combustível queimado.
No segundo caso, temos que calcular a taxa de calor liberada na combustão com de excesso de ar dividida pela quantidade de de combustível queimado. Quando a questão diz que de excesso de ar é consumido na combustão, isso significa que foi utilizado de ar teórico na combustão.
Relaxa que a importância dessa porcentagem de ar teórico vai ficar mais clara mais pra frente.
Para achar e , temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é trocado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar e vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Vamos primeiro resolver a pimeira situação! Logo, começamos a calcular as vazões molares, escrevendo a equação química da combustão do primeiro caso que não tem excesso de ar.
A combustão completa de sem excesso de ar gera apenas , e como produto. Ou seja, nessa combustão , do ar e do ar reagem pra formar , e .
onde , , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar do combustível .
Nós podemos escolher escrever a equação química pra de combustível pra facilitar a nossa vida. Podemos fazer isso, porque não vai interferir no valor final de .
Ou seja, podemos escrever a equação pra igual . Com isso a vazão molar de combustível vale:
A partir desse valor conseguimos encontrar os coeficientes restantes!
O coeficiente é encontrado através do balanço de carbono . Para a quantidade de ficar balanceada, os de dos reagentes e os de dos produtos devem ser iguais.
Já o coeficiente é determinado por meio do balanço do hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes têm que ser iguais aos de dos produtos.
Por fim, o coeficiente é calculado através do balanço de . Nesse balanço, os de dos reagentes têm que ser iguais aos de dos produtos.
A vazão molar de dos reagentes é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à e a vazão molar de é igual à .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 3
As entalpias de formação de e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! Precisamos pegar o valor da entalpia de formação de líquido!
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia . No entanto, é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os produtos e reagentes estão a , vale zero pra todas as substâncias.
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 4
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Como sabemos que a vazão molar de combustível vale , podemos achar .
Beleeeza, pessoal! Encontramos a taxa de calor dividida pela vazão molar pra situação 1. Falta achar o vaor dessa divisão pra situação 2. Vamos começar os cálculos no próximo passo!
Passo 5
Galera, vocês podem estar desesperados achando que vamos precisar calcular tuuuudo de novo pra situação 2, mas calminha! Temos sim que achar os somatórios das entalpias dos reagentes e dos produtos . No entanto, nós já conhecemos os valores de e dos reagentes e produtos!
Logo, a única coisa que precisamos fazer é achar as vazões molares da combustão completa com excesso de ar. Fazemos isso, balanceando a equação de combustão do abaixo.
onde , , , , e são os coeficientes estequiométricos da combustão com excesso de ar.
Esses coeficientes são iguais às vazões molares da combustão comexcesso de ar! Por exemplo, o coeficiente do combustível é igual à vazão molar do combustível .
Nós podemos escolher escrever a equação química pra de combustível pra facilitar a nossa vida. Podemos fazer isso, porque não vai interferir no valor final de .
Ou seja, podemos escrever a equação pra igual . Com isso a vazão molar de combustível vale:
O coeficiente é encontrado de um jeito diferente. Calculamos a partir do valor de !
Quando a questão diz que o combustível é queimado completamente com de ar teórico, ela quer dizer que o coeficiente é igual a de .
Pronto, achamos o coeficiente através da porcentagem de ar teórico!
Para achar os outros coeficientes, vamos fazer o balanço da equação de reação no próximo passo.
Passo 6
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de dos reagentes é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à , a vazão molar de é igual à e a vazão molar do dos produtos é igual a .
Pronto! Achamos as vazões molares. Agora podemos partir pro cálculo dos somatórios!
Passo 7
O somatório de entalpias que aparece no lado esquerdo da equação da primeira lei se encontra abaixo.
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita.
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Como sabemos que a vazão molar de combustível vale , podemos achar .
Uhuuuuuul! Acabamos a questão! E olha só que interessante: o valor das taxas de calor não foi alterado com o excesso de ar. Isso aconteceu, porque o exercício disse que esse ar em excesso entra e sai da câmara de combustão com a mesma temperatura de . Isso quer dizer que esse excesso de ar não absorveu energia e não influenciou no calor trocado!
Loucura, né pessoal? A termodinâmica é mesmo belíssima!
Resposta
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 804-15-65(c)
Propano gasoso é queimado em um processo de regime permanente à pressão constante de com de ar teórico. Durante o processo de combustão, do carbono no combustível é convertido em e é convertido em . Determine
- a transferência de calor da câmara de combustão (em ), depois que de combustível são queimados quando os reagentes entram na câmara de combustão a e os produtos são resfriados a .
Passo 1
Galera, esse é um exercício de combustão que pede pra gente calcular o calor liberado por do combustível .
Para calcular esse calor a questão diz que foi utilizado de ar teórico na combustão.
Relaxa que a importância dessa porcentagem de ar teórico vai ficar mais clara mais pra frente.
Para achar , temos que usar a primeira lei da termodinâmica adaptada à combustão. No entantp, a equação abaixo não é a equação presente na teoria. Como a questão quer saber o calor e não a taxa de calor , substituímos por , por e por .
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados e o somatório da direita é a soma das entalpias dos produtos que são gerados. é o trabalho realizado. Ele vale zero, porque o enunciado só diz que calor é trocado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as quantidades de presentes nesses somatórios. Então vamos começar as contas tentando encontrar essas quantidades de .
Passo 2
O primeiro passo para achar essas quantidades de é escrever a equação da reação. Pra isso, devemos conhecer os reagentes e produtos. No nosso caso, a questão disse que e ar seco reagem na combustão. Logo, , do ar e do ar são os reagentes. Os produtos são , , e . Veja a equação dela abaixo.
, , , , , e são os coeficientes estequiométricos da combustão do enunciado.
Esses coeficientes são as quantidades de de cada substância. Por exemplo, o coeficiente do combustível é igual à quantidade de do combustível .
Como a questão nos diz que de combustível são queimados, é igual a . Com isso a quantidade de de combustível vale:
Ou seja, encontrar as quantidades de é a mesma coisa que encontrar os coeficientes estequiométricos da combustão. No entanto, para calcular o valor do coeficiente , temos que descobrir o valor que o coeficiente teria, caso a combustão fosse completa e sem excesso de ar. Faremos isso no próximo passo!
Passo 3
A combustão completa de sem excesso de ar gera apenas , e como produto. Ou seja, nessa combustão , do ar e do ar reagem pra formar , e .
onde , , e são os coeficientes estequiométricos da combustão completa sem excesso de ar. O coeficiente é encontrado através do balanço de carbono . Para a quantidade de ficar balanceada, os de dos reagentes e os de dos produtos devem ser iguais.
Já o coeficiente é determinado por meio do balanço do hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes têm que ser iguais aos de dos produtos.
Tá, achamos o coeficiente . Mas como encontramos o coeficiente a partir de ?
Quando a questão diz que o combustível é queimado completamente com de ar teórico, ela quer dizer que o coeficiente é igual a de .
Pronto, achamos o coeficiente através da porcentagem de ar teórico!
Para achar os outros coeficientes, vamos fazer o balanço da equação de reação no próximo passo.
Passo 4
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem virar de e de !
Veja a equação de combustão abaixo para lembrar.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A quantidade de de dos reagentes é igual à , a quantidade de de dos reagentes e dos produtos é igual a , a quantidade de de é igual à , a quantidade de de é igual à , a quantidade de de é igual a e a quantidade de de nos produtos é igual à .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 5
As entalpias de formação de e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! A água dos produtos está a e não sabemos quanto dessa água é vapor e quanto é líquido. Como a temperatura é baixa, podemos supor que parte do vapor d’água condensou. Logo, a água está saturada na pressão de saturação pra .
Esse valor de pressão é encontrado na tabela de saturação da água pra !
Essa é a pressão parcial da água no produto.
Pra achar a quantidade de de vapor d’água, temos que usar a fórmula da pressão parcial.
A fórmula acima diz que essa pressão é igual à pressão total atmosférica dos produtos vezes a fração molar de nos produtos. Essa fração molar é igual à quantidade de dividida pela soma dos coeficientes dos produtos que são vapor.
Substituindo na fórmula da pressão parcial:
A quantidade de água líquida é igual à quantidade total de água menos a quantidade de vapor d’água.
Ou seja, tem realmente um pouquinho de água líquida e um pouquinho de vapor d’água água. Logo, precisamos da entalpia de formação de na forma líquida e de vapor. Pegaremos esse valor na tabela no passo seguinte!
Passo 6
As entalpias de formação das substâncias restantes valem:
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia . No entanto, é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os produtos e reagentes estão a , vale zero pra todas as substâncias.
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 7
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas quantidades de dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos pelas quantidades de dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Boaaaa! Fim de papo! Acabamos com a questão!
Resposta
Exercício Resolvido #6
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 803-15.58
Em um determinado processo de combustão, n-octano gasoso é queimado com de excesso de ar em um queimador de pressão constante. O ar e o combustível entram nesse queimador de forma constante nas condições padrão, e os produtos de combustão saem a . Calcule a transferência de calor, em de combustível, durante essa combustão.
Passo 1
Então, galera, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível dividida pela massa de combustível queimada a cada segundo .
Pra calcular essa divisão, a questão diz que de excesso de ar é consumido na combustão. Isso significa que foi utilizado de ar teórico na combustão.
Relaxa que a importância dessa porcentagem de ar teórico vai ficar mais clara mais pra frente.
Para achar , temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é trocado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Começamos a calcular as vazões molares, escrevendo a equação química da combustão.
O enunciado diz que a combustão teve muito excesso de ar. Logo, a combustão foi completa e gerou , , e como produto. Como o ar é composto por e , o , o e o são os reagentes.
onde , , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar do combustível .
Nós podemos escolher escrever a equação química pra de combustível pra facilitar a nossa vida. Podemos fazer isso, porque não vai interferir no valor final de .
Ou seja, podemos escrever a equação pra igual . Com isso a vazão molar de combustível vale:
A partir desse valor e do valor da porcentagem de ar teórico que o enunciado nos informou, podemos descobrir o coeficiente da equação química. Faremos isso no próximo passo!
Passo 3
Pra encontrar o coeficiente , temos que descobrir o valor que ele teria caso a combustão não tivesse excesso de ar. Ou seja, precisamos achar o valor do coeficiente para o caso da combustão ser completa sem a geração de nos produtos, como mostrado abaixo.
onde , , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Para encontrar , devemos encontrar antes e . O coeficiente é encontrado através do balanço de carbono . Para a quantidade de ficar balanceada, os de dos reagentes e os de dos produtos devem ser iguais.
Já o coeficiente é determinado por meio do balanço do hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes têm que ser iguais aos de dos produtos.
Tá, achamos o coeficiente . Mas como encontramos o coeficiente a partir de ?
Quando a questão diz que o combustível é queimado completamente com de ar teórico, ela quer dizer que o coeficiente é igual a de .
Pronto, achamos o coeficiente através da porcentagem de ar teórico!
Para achar os outros coeficientes, vamos fazer o balanço da equação de reação no próximo passo.
Passo 4
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de dos reagentes é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à , a vazão molar de é igual à , a vazão molar do dos produtos é igual a .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 5
As entalpias de formação de e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! Precisamos pegar o valor da entalpia de formação de vapor de !
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia no passo seguinte!
Passo 6
é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os reagentes estão a , o dos reagentes vale zero.
Pra encontrar o dos produtos, temos que converter a temperatura dos produtos de pra . Fazemos isso, somando à temperatura!
Os valores de para os produtos são determinados por tabelas. Nem sempre temos a disposição tabelas com valores de . As vezes, as tabelas mostram o valor da entalpia na temperatura de e o valor da entalpia na temperatura de e nós temos que calcular subtraindo esses dois valores.
Então, vamos resolver esse exercício como se a gente só tivesse esse tipo de tabela a disposição!
Vamos iniciar achando de dos produtos.
de dos produtos vale:
de dos produtos vale:
de dos produtos vale:
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 7
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Temos agora que calcular a massa de combustível queimada a cada segundo. Fazemos isso, multiplicando pela massa molar do combustível que vale .
Dividindo pela vazão de combustível :
Uhuuuuuul! Esse exercício foi mais demorado, mas valeu a pena fazer! Aprendemos muito!
Resposta
Exercício Resolvido #7
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 803-15.57
Combustível propano é queimado com uma razão ar/combustível de em um forno aquecido à pressão atmosférica. Determine a transferência de calor por quilograma de combustível queimado, considerando que a temperatura dos produtos é tal que a água líquida só começa a se formar nos produtos.
Passo 1
Então, galera, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível dividida pela massa de combustível queimada a cada segundo .
Pra calcular essa divisão, a questão diz que a razão ar-combustível vale . Isso quer dizer que a massa de ar que é usada na combustão a cada segundo dividida pela massa de combustível queimado a cada segundo vale .
Para achar , temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é trocado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Começamos a calcular as vazões molares, escrevendo a equação química da combustão. Quando o enunciado nos dá sem falar se a combustão é completa ou não, é porque a combustão é completa com excesso de ar! Logo, os produtos são , , e . Como o ar é composto por e , o , o e o são os reagentes.
onde , , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar do combustível .
Nós podemos escolher escrever a equação química pra de combustível pra facilitar a nossa vida. Podemos fazer isso, porque não vai interferir no valor final de .
Ou seja, podemos escrever a equação pra igual . Com isso a vazão molar de combustível vale:
A partir desse valor e do valor de , podemos descobrir o coeficiente da equação química. Faremos isso no próximo passo!
Passo 3
Primeiro, temos que calcular a massa de combustível queimada a cada segundo. Fazemos isso, multiplicando pela massa molar do combustível que vale .
Agora, podemos achar a massa de ar usada a cada segundo na combustão através da fórmula de .
Dividindo essa vazão de ar pela massa molar do ar, achamos a vazão molar de ar. vale .
Como o ar é composto por de e de , podemos calcular a quantidade de consumida a cada segundo, somando a quantidade de de com a quantidade de de .
Pronto, achamos o coeficiente através da fórmula de !
Para achar os outros coeficientes, vamos fazer o balanço da equação de reação no próximo passo.
Passo 4
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de dos reagentes é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à , a vazão molar de é igual à e a vazão molar do dos produtos é igual a .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios! Além disso, é necessário achar antes a temperatura dos produtos! É necessário achar pra achar .
Passo 5
O enunciado diz que que a temperatura dos produtos é tal que a água líquida só começa a se formar nos produtos. Isso quer dizer que a temperatura dos produtos é a temperatura de saturação da água. Ou seja, pra saber quanto vale , temos que saber quanto vale a pressão parcial da água. A fórmula de se encontra abaixo.
A fórmula acima diz que essa pressão é igual à pressão total atmosférica dos produtos vezes a fração molar de nos produtos. Essa fração molar é igual ao coeficiente da água dividido pela soma dos coeficientes dos produtos.
Substituindo na fórmula de :
Agora, podemos usar a tabela d esaturação da água para acharmos a temperatura de saturação da pressão . Como a tabela não possui o valor de temperatura de saturação para essa pressão exata, interpolaremos a tabela.
Somando a essa temperatura , achamos o valor de em kelvin .
Para facilitar as próximas etapas de cálculo e evitar interpolações, vamos arredondar a temperatura para . Isso pode ser feito, porque a diferença de valores é bem pequena! Cuidado pra não arredondar valores muito diferentes!
Agora vamos partir pro cálculo de e !
Passo 6
As entalpias de formação de e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! Precisamos pegar o valor da entalpia de formação de vapor de !
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia no passo seguinte!
Passo 7
é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que os reagentes são queimados em condições atmosféricas, os reagentes estão a . Logo o dos reagentes vale zero.
Os valores de para os produtos são determinados por tabelas. Nem sempre temos a disposição tabelas com valores de . As vezes, as tabelas mostram o valor da entalpia na temperatura de e o valor da entalpia na temperatura de e nós temos que calcular subtraindo esses dois valores.
Então, vamos resolver esse exercício como se a gente só tivesse esse tipo de tabela a disposição!
Vamos iniciar achando de dos produtos.
de dos produtos vale:
de dos produtos vale:
de dos produtos vale:
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 8
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Dividindo pela vazão de combustível :
Chegamos na resposta! Agoooora sim pode sorrir e comemorar essa vitória com a família!
Resposta
Exercício Resolvido #8
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 804-15.59
Combustível propano a é misturado continuamente com de excesso de ar a em uma câmara de combustão à pressão atmosférica. Os produtos da combustão saem a , e a vazão volumétrica de ar é de . Determine a taxa de transferência de calor nesse combustor.
Passo 1
Então, galera, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível.
Pra calcular , a questão diz que de excesso de ar é consumido na combustão. Isso significa que foi utilizado de ar teórico na combustão.
Relaxa que a importância dessa porcentagem de ar teórico vai ficar mais clara mais pra frente.
Para achar , temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é trocado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Começamos a calcular as vazões molares, escrevendo a equação química da combustão.
O enunciado diz que a combustão teve muito excesso de ar. Logo, a combustão foi completa e gerou , , e como produto. Como o ar é composto por e , o , o e o são os reagentes.
onde , , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar desse combustível .
Isso quer dizer que achar as vazões molares é a mesma coisa que achar os coeficientes.
No entanto, para encontrar a vazão molar , temos que encontrar a vazão molar de ar primeiro.
Achamos usando a equação P-V-T de gases perfeitos mostrada abaixo.
onde é a pressão do ar que é igual à pressão atmosférica segundo o enunciado. Logo, vale:
é a constante universal dos gases. Ela vale . é a temperatura do ar em kelvin . Logo, temos que converter a temperatura de pra , somando à temperatura.
é a vazão volumétrica de ar que vale segundo o enunciado.
Repare que essa equação P-V-T de gases perfeitos usa a vazão volumétrica do gás ao invés de usar o volume do gás. Nós fazemos essa mudança, quando queremos calcular a vazão molar do gás ao invés de calcular a quantidade de mol do gás! Substituindo os dados:
No próximo passo, nós vamos aprender a achar a vazão molar de combustível a partir da vazão molar de ar .
Passo 3
Com a vazão molar de ar somos capazes de ar o coeficiente .
Como o ar é formado por e , a vazão molar de ar é a soma entre a vazão molar de e a vazão molar de . Logo:
Substituindo o valor de , achamos o valor de .
Esse coeficiente é a vazão molar de ! Além disso, achar o coeficiente é fundamental pra achar a vazão molar do combustível! Veremos agora o motivo!
Quando a questão diz que o combustível é queimado completamente com de ar teórico, ela quer dizer que a vazão molar de é vezes maior que a vazão que o teria caso a combustão não tivesse excesso de ar.
Agora, pra achar o coeficiente , temos que equilibrar a equação de combustão sem excesso de ar de .
Ou seja, precisamos achar o valor do coeficiente para o caso da combustão ser completa sem a geração de nos produtos, como mostrado abaixo.
onde , , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Para encontrar , devemos encontrar antes e . O coeficiente é encontrado através do balanço de carbono . Para a quantidade de ficar balanceada, os de dos reagentes e os de dos produtos devem ser iguais.
Já o coeficiente é determinado por meio do balanço do hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes têm que ser iguais aos de dos produtos.
Substituindo o valor de :
Pronto, achamos o coeficiente !
Para achar os outros coeficientes da combustão com excesso de ar, vamos fazer o balanço da equação de reação no próximo passo.
Passo 4
Os coeficientes restantes da combustão com excesso de ar são encontrados através do balanço da equação abaixo.
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de dos reagentes é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à , a vazão molar de é igual à e a vazão molar do dos produtos é igual a .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 5
As entalpias de formação de e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! Precisamos pegar o valor da entalpia de formação de vapor de , porque os produtos de combustão estão muito quentes (estão a ).
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia nos passos seguintes!
Passo 6
é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que está a , o de vale zero.
Pra encontrar o dos reagentes que restam, temos que converter a temperatura desses reagentes de pra . Fazemos isso, somando à temperatura!
Os valores de para os produtos são determinados por tabelas. Nem sempre temos a disposição tabelas com valores de . As vezes, as tabelas mostram o valor da entalpia na temperatura de e o valor da entalpia na outra temperatura de e nós temos que calcular subtraindo esses dois valores.
Então, vamos resolver esse exercício como se a gente só tivesse esse tipo de tabela a disposição! Repare que as tabelas que usaremos não têm os valores de entalpia para a temperatura de . Ou seja, precisaremos interpolar as tabelas pra achar !
Vamos iniciar achando de dos reagentes.
de dos reagentes vale:
No próximo passo nós vamos descobrir os valores de dos produtos!
Passo 7
Pra encontrar o dos produtos, temos que converter a temperatura desses produtos de pra . Fazemos isso, somando à temperatura!
Os valores de para os produtos são determinados por tabelas. Nem sempre temos a disposição tabelas com valores de . As vezes, as tabelas mostram o valor da entalpia na temperatura de e o valor da entalpia na outra temperatura de e nós temos que calcular subtraindo esses dois valores.
Preste atenção! As tabelas que usaremos também não têm os valores de entalpia para a temperatura de . Ou seja, precisaremos interpolar de novo as tabelas pra achar !
Vamos iniciar achando de dos produtos.
de dos produtos vale:
de dos produtos vale:
de dos produtos vale:
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 8
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Menin@ do céu! Quanto trabalho!
Pois é.... exercícios de primeira lei da combustão são mais demoradinhos mesmo. Mas esses são os exercícios que podem cair na sua prova. Então vale muito a pena fazer!