Razão Ar-Combustível e Razão Combustível-Ar
Produzido por Rafael Cardoso BrandãoTeoria
As quantidades de ar e combustível devem ser equilibradas!
Quando sopramos uma vela muito forte, o fogo dela apaga. Ou seja, muito ar faz o combustível da vela parar de queimar. Quando tampamos a vela com um copo, o fogo dela também apaga. Nesse caso, a falta de ar faz o combustível da vela parar de queimar também. Por que uma hora o ar faz a combustão parar e outra hora ele é necessário para a combustão?
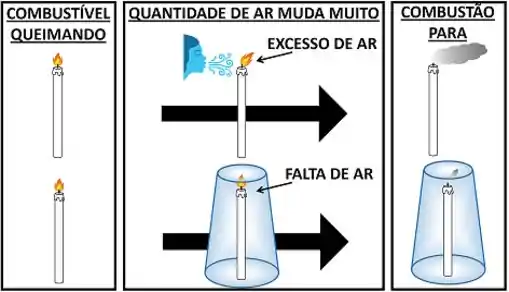
Porque a combustão precisa de uma proporção equilibrada entre ar e combustível para dar certo. Se a reação possui muito ar e pouco combustível, ela não dá certo. Por outro lado, se a reação possui mais combustível e pouco ar, ela também dá errado. Isso significa que a proporção precisa estar em uma faixa de valores para a combustão dar certo.
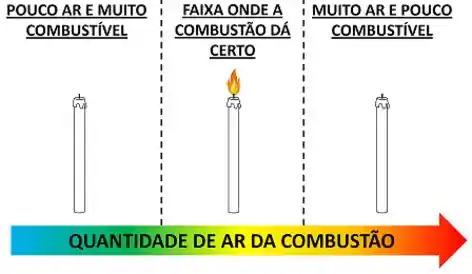
Por causa disso, é muito importante saber calcular qual é a proporção entre ar e combustível que está presente entre os reagentes da combustão! Mas como se faz isso?
É isso que veremos agora!
Razão ar-combustível
Nós calculamos a proporção entre ar e combustível presentes numa combustão, dividindo a quantidade de ar pela quantidade de combustível. O resultado dessa divisão é chamado de relação ar-combustível ou razão ar-combustível. Geralmente, essa razão é calculada como a massa de ar dividida pela massa do combustível .
onde:
- é a razão ar-combustível em base mássica;
- é a massa de ar presente nos reagentes. Sua unidade no Sistema Internacional (S.I.) é o quilograma ;
- é a massa de combustível presente nos reagentes. Sua unidade no Sistema Internacional (S.I.) é o quilograma .
Quando calculamos a razão ar-combustível através das massas , dizemos que está em base mássica. No entanto, essa não é a única forma de calcularmos . Ela também pode ser calculada como a divisão entre a quantidade de do ar dividida pela quantidade de de combustível . Nesse caso dizemos que está em base molar !
onde:
- é a razão ar-combustível em base molar;
- é a quantidade de do ar presente entre os reagentes;
- é a quantidade de do ar presente entre os reagentes.
Nós vamos ver através dos exercícios que calcular é, geralmente, mais fácil do que calcular . No entanto, muitas questões pedem o valor de em base mássica . Então como podemos converter o valor de para ? A fórmula abaixo faz essa mudança de base pra gente!
onde:
- é a massa molar do ar. Ela vale aproximadamente .
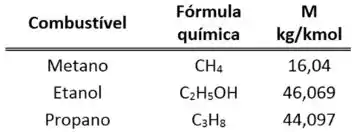
- é a massa molar do combustível. Ela varia de combustível para combustível. A tabela abaixo mostra o valor da massa molar para alguns combustíveis.
Exemplo de cálculo da razão ar-combustível
Já conhecemos as fórmulas para calcular a razão ar-combustível a partir das quantidades de do ar e do combustível . Mas como a gente pode achar o valor de se as questões de combustão quase nunca informam diretamente os valores de e pra gente? Para tirar essa dúvida, vamos resolver um exemplo!

Determine a razão ar-combustível em base mássica da combustão representada pela equação química abaixo.
O primeiro passo para calcular a razão ar-combustível em base mássica é calcular a razão ar-combustível em base molar . A fórmula de depende da quantidade de do combustível e da quantidade de de ar . O combustível da equação química acima é o metano . A quantidade de do metano na equação vale:
Já a quantidade de de ar é a soma entre a quantidade de de nitrogênio e a quantidade de do oxigênio .
Dividindo essas duas quantidades, obtemos o valor de .
Esse valor de significa que para cada de existem de ar reagindo com ele! Em outras palavras o valor de informa pra gente a quantidade de de ar que reage com cada de combustível!

Podemos calcular , convertendo o valor de com a ajuda das massas molares do ar e do metano . A massa molar do metano está presente na tabela de massa molar de alguns combustíveis mostrada antes.
O valor de significa que, nessa reação, para cada de existem de ar reagindo com ele! Dizendo isso de outra forma, para cada de combustível existem de ar reagindo com ele!
Razão combustível-ar (CA)
Aprendemos algumas formas de calcular a razão ar-combustível , mas ela não é a única forma de calcular a proporção entre combustível e ar!

A gente também pode calcular a proporção entre combustível e ar, dividindo a quantidade de combustível pela quantidade de ar. Essa divisão é chamada de razão combustível-ar ou relação combustível-ar .
onde:
- é a razão combustível-ar em base mássica;
- é a razão combustível-ar em base molar.
Mas qual é a diferença entre essa forma nova de calcular a proporção entre combustível e ar e a outra forma mais comum de aparecer em exercícios ?
A razão combustível-ar é o inverso da razão ar-combustível ! Ou seja, a gente calcula invertendo a fórmula de .
Por causa disso, a forma de ler o valor da razão combustível-ar é diferente da forma de ler o valor da razão ar-combustível ! Então vamos aprender a ler esse valor e aprender a calcular , resolvendo um exemplo!
Exemplo de cálculo da razão combustível-ar
Determine a razão combustível-ar em base mássica e em base molar da combustão representada pela equação química abaixo.
Essa equação química é igual à equação química que usamos de exemplo para calcular . Isso significa que os valores de e que calculamos antes, serve para o exemplo de agora também!
Logo, para achar , só precisamos inverter o valor de que já calculamos!
Esse valor de significa que para cada de ar existem de reagindo com ele! Em outras palavras o valor de informa pra gente a quantidade de de combustível que reage com cada de ar!
Podemos usar o mesmo truque de inverter a fórmula de para achar !
O valor de significa que para cada de ar existem de reagindo com ele! Em outras palavras o valor de informa pra gente a quantidade de de combustível que reage com cada de ar!