Teoria
O que é a radiação?
Na transferência de calor por condução, o calor é trocado através da colisão entre moléculas. Na transferência de calor por convecção, o calor é trocado por causa da colisão entre moléculas e por causa do movimento do fluido que carrega o calor. Isso quer dizer que, nesses dois casos, o calor precisa ser trocado com a ajuda de moléculas.
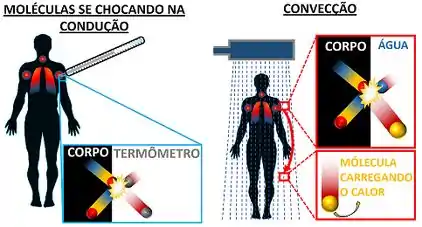
No entanto, nem toda forma de trocar calor precisa da ajuda de moléculas para acontecer. Esse é o caso, por exemplo, do calor que a Terra recebe do Sol. Como o calor que o Sol emite consegue chegar na Terra, se o espaço que separa os dois astros não possui nenhuma molécula para ajudar a transportar esse calor?

A energia do Sol é emitida na forma de ondas eletromagnéticas. Como esse tipo de onda não precisa da ajuda de moléculas para se propagar, elas conseguem viajar pelo vácuo do espaço até chegar na Terra! A energia emitida por um objeto na forma de onda eletromagnética é chamada de radiação! Mas como podemos calcular a taxa de calor emitida por radiação?
Lei de Stefan-Boltzmann para um corpo negro
A taxa máxima de radiação que a superfície de um objeto pode emitir é calculada pela fórmula abaixo. Essa fórmula é chamada de lei de Stefan-Boltzmann. Ou seja, a lei de Stefan-Boltzmann calcula a máxima taxa de calor por radiação emitida pela superfície de um objeto!
onde:
- é a máxima taxa de calor teórica que a superfície um objeto pode emitir. Na vida real, nenhuma superfície consegue emitir tanto calor por radiação quanto . Em outras palavras, é apenas um limite máximo teórico que não é alcançado na prática. Sua unidade no Sistema Internacional (S.I.) é o watt ;
- é a constante de Stefan-Boltzmann. Seu valor é igual para todas as superfícies e todos os objetos. Abaixo é mostrado o valor dessa constante com a unidade de acordo com o Sistema Internacional (S.I.).
- é a temperatura da superfície do objeto. As questões de radiação da termodinâmica geralmente consideram que toda a superfície do objeto possui a mesma temperatura . A unidade de segundo o Sistema Internacional (S.I.) é o kelvin . Ou seja, NUNCA coloque o valor de em grau Celsius na fórmula!
- é a área da superfície que está emitindo radiação a uma temperatura igual a . Sua unidade segundo o Sistema Internacional (S.I.) é o metro quadrado .
- é a taxa de calor emitida por radiação pela superfície real. Sua unidade no Sistema Internacional (S.I.) é o watt ;
- é a emissividade da superfície. Essa variável mede o quanto uma superfície se aproxima de um corpo negro. Seus valores vão de a . Se valer , a superfície é um corpo negro! Se valer , a superfície não emite radiação. não possui unidade!


A superfície teórica que consegue emitir radiação a uma taxa igual a é chamada de corpo negro. Isso quer dizer que apenas a superfície ideal chamada de corpo negro pode emitir calor por radiação a uma taxa . Além disso, a radiação emitida por um corpo negro é chamada de radiação de corpo negro.
Exemplo de cálculo da taxa de radiação emitida por um corpo negro
Determine a taxa de radiação emitida por um corpo negro esférico com diâmetro igual a . Considere que a superfície do corpo negro está a .
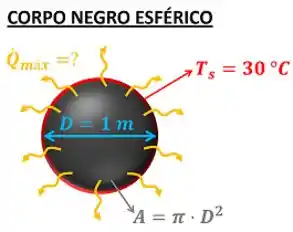
O primeiro passo para calcular essa taxa de radiação é converter a temperatura dada em grau Celsius para kelvin . Fazemos isso, somando ao valor da temperatura em grau Celsius .
O segundo passo é calcular a área da superfície que se encontra a temperatura de . Como o enunciado disse que o corpo negro é esférico, a área da superfície é igual à área de uma esfera com de diâmetro.
Substituindo esses valores na lei de Stefan-Boltzmann, encontramos:
Isso quer dizer que esse corpo negro emite calor por radiação a uma taxa igual a .
Acabamos de aprender a calcular o valor máximo de calor que um objeto esférico a com de diâmetro pode emitir. Mas como podemos calcular a taxa de radiação real emitida pela superfície de um objeto?
Veremos isso agora!
Fórmula para calcular a taxa de radiação emitida por uma superfície real
A fórmula para calcular a taxa de radiação emitida por uma superfície real é muito parecida com a fórmula para um corpo negro! A única diferença entre as duas é que a fórmula da superfície real possui um termo a mais. Esse termo é chamado de emissividade da superfície. Esse termo é representado pela letra grega . A fórmula de se encontra abaixo.
onde:

Já que descobrimos a fórmula que calcula a taxa de radiação emitida por uma superfície real, vamos resolver um exemplo de superfície real para exercitar!
Exemplo de cálculo da taxa de radiação emitida por uma superfície real
Vamos atualizar o exemplo da esfera a com diâmetro de que emite radiação. Vamos imaginar agora, que essa é uma esfera real de cobre. Considerando que a emissividade do cobre vale , determine a taxa de radiação emitida pela superfície do cobre.
A área e a temperatura já foram calculadas no exemplo passado!
A emissividade foi informada pelo próprio enunciado.
Substituindo esses valores na fórmula de , achamos:
Perceba a diferença entre o caso real da esfera de cobre e o caso ideal do corpo negro esférico !
No entanto, nem sempre essa diferença entre essas duas taxas é tão grande. Esse foi apenas o caso de uma esfera de cobre polido.
Existe vários outros casos que podemos estudar! Então que tal a gente resolver exercícios passo a passo de radiação?
Lei de Stefan-Boltzmann para um corpo negro
Exemplo de cálculo da taxa de radiação Q ˙ m á x á emitida por um corpo negro
Fórmula para calcular a taxa de radiação emitida por uma superfície real Q ˙
Exemplo de cálculo da taxa de radiação Q ˙ emitida por uma superfície real
Exercícios Resolvidos
Exercício Resolvido #1
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 97-4.104
A superfície de uma tora de madeira, que está localizada em uma fornalha, é . Admitindo que a emissividade da superfície da tora seja igual a (corpo negro perfeito), determine a taxa de emissão de energia por radiação na superfície da tora.
Passo 1
Fala, gente! Partiu fazer um exercício de radiação pra gravar bem a matéria?

Essa questão quer saber quanto vale a taxa de calor emitida por radiação por uma tora dividida pela área da superfície da tora. Em outras palavras, a questão quer saber quanto vale . A figura abaixo mostra os dados que temos para calcular esse valor.
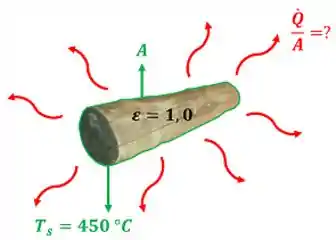
é a emissividade da superfície da tora de madeira e é a temperatura da superfície da tora de madeira.
Para calcular a taxa de calor emitida pela radiação de uma superfície, temos sempre que usar a lei de Stefan-Boltzmann mostrada abaixo.
Agora que sabemos de tudo isso, podemos partir pro cálculo de no próximo passo.
Passo 2
Antes de atacar o problema e substituir os valores que temos na fórmula, temos que lembrar de uma regra muito importante que precisamos seguir pra utilizar a lei de Stefan-Boltzmann corretamente! Essa regra diz que a temperatura tem SEMPRE que estar em kelvin pra usarmos essa equação. Pra converter de pra , precisamos somar à temperatura!
Além disso, precisamos lembrar que a constante de Stefan-Boltzmann vale SEMPRE .
Agora sim podemos substituir os valores na equação que temos e achar .
Uhuuuul! Achamos o resultado da questão! Arrasamos!
Resposta
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 97-4.105
Um aquecedor por radiação cilíndrico apresenta comprimento e diâmetro igual a e . A potência dissipada no aquecedor é . Admitindo que a emissividade da superfície do aquecedor seja igual a e desprezando a radiação que incide no aquecedor, determine a temperatura superficial deste aquecedor.
Passo 1
Fala, gente! Partiu fazer um exercício de radiação pra gravar bem a matéria?

Essa questão quer saber quanto vale a temperatura superficial de um aquecedor que emite uma taxa de calor por radiação de . A figura abaixo mostra os dados que temos para calcular .
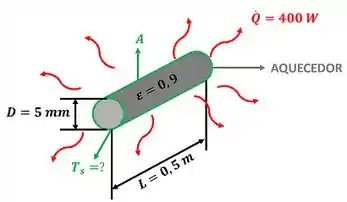
é a emissividade da superfície do aquecedor, é a área da superfície do aquecedor, é o comprimento do aquecedor e é o diâmetro do aquecedor.
Para calcular a temperatura de uma superfície que emite radiação, temos sempre que usar a lei de Stefan-Boltzmann mostrada abaixo.
Reorganizando a equação:
Agora que sabemos de tudo isso, podemos partir pro cálculo de no próximo passo.
Passo 2
Antes de atacar o problema e substituir os valores que temos na fórmula, temos que lembrar de calcular a área em . Pra isso, usamos a fórmula que calcula a área total de um cilindro presente na figura abaixo.
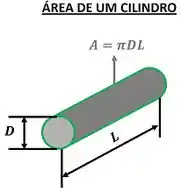
Além disso, precisamos converter a unidade do diâmetro de pra , dividindo por .
Lembrando que a constante de Stefan-Boltzmann vale sempre , podemos substituir os dados na fórmula de e achar logo esse valor. Mas ATENÇÃO! A temperatura calculada a partir da lei de Stefan-Boltzmann está sempr em kelvin . Logo, o resultado que vamos obter será em !
Isso aííííí! Resolvemos o exercício! Mandamos muito!
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 97-4.103
A temperatura e a emissividade da superfície externa de uma casa são iguais a e . A temperatura e a emissividade média do ambiente que circunda a casa são igual a e . Determine a taxa de emissão de radiação por unidade de área na superfície externa da casa e no ambiente.
Passo 1
Oi, gente! Como vão? Estudando radiação pra tirar 10 na prova?
Essa questão de radiação pede que a gente calcule dois termos. Ela quer que a gente ache o valor da taxa de calor por unidade de área emitida por radiação por uma casa e pede que a gente ache a taxa de calor por unidade de área emitida por radiação pelo ambiente.
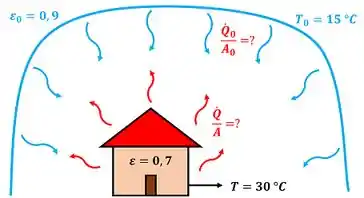
e são a emissividade e temperatura da superfície da casa respectivamente. e são a emissividade e a temperatura do ambiente.
Pra calcular e da radiação, usamos a lei de Stefan Boltzmann. Escrevemos abaixo a lei de Stefan Boltzmann pra casa e pro ambiente.
Com essas duas equações e os dados da figura, já somos capazes de calcular e no próximo passo.
Passo 2
Pra achar e precisamos lembrar que a constante de Stefan-Boltzmann vale sempre . Além disso, temos que lembrar que as temperaturas e tem SEMPRE que estar em kelvin pra usarmos essas equações. Pra converter de pra , precisamos somar às temperaturas! Com isso em mente, vamos achar primeiro.
Opa! Já achamos um dos valores que o enunciado pediu! Agora vamos achar !
Feshoooow! Acabamos com a questão! Já estamos ficando muito craques em radiação! :)
Resposta
Exercício Resolvido #4
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 109-2-142
Uma superfície preta, quente, e de a está perdendo calor por convecção para o ar ambiente a com um coeficiente de transferência de calor por convecção de , e por radiação para as superfícies vizinhas a . A taxa total com a qual calor é perdido a partir da superfície é
Passo 1
Oi, galera bonita, prontos pra essa questão que mistura convecção com radiação?
O enunciado pede para a gente calcular a taxa de calor que uma superfície preta perde de duas formas. Uma parte de , que chamaremos de , a superfície preta perde por convecção. Essa parte é calculada com a lei de resfriamento de Newton abaixo.
onde é o coeficiente de transferência de calor por convecção de , é a área da superfície que vale , é a temperatura da superfície que vale e é a temperatura do ar a .
A outra parte de é perdida por radiação e é calculada abaixo:
Essa fórmula mostra que, pra gente calcular a parcela que a superfície perde por radiação, temos que calcular a quantidade que ela perde por emitir radiação menos a quantidade que ela ganha por absorver radiação das superfícies ao redor! Essas duas taxas são calculadas através da lei de Stefan-Boltzmann. Vamos iniciar as contas no passo seguinte!
Passo 2
Vamos iniciar as contas, calculando a taxa de calor que a superfície perde por convecção.
Fazemos isso, substituindo os dados que temos na fórmula de do passo 1.
No próximo passo calcularemos !
Passo 3
Pra calcular a parcela de taxa de calor que a superfície perde por radiação, temos que achar a taxa que ela emite por radiação. A equação abaixo calcula esse valor.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície preta. O enunciado informou o valor dessa emissividade de forma indireta! Quando ele disse que a superfície é preta, ele quis dizer que a superfície era um corpo negro. Logo, ele quis dizer que essa superfície possui emissividade igual a .
Para achar só falta converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Agora só falta achar pra calcular e !
Passo 4
Para calcular a taxa de calor emitida por radiação que o corpo negro absorve, temos que saber que um corpo negro absorve toda a radiação que incide sobre ele. Logo, a radiação emitida pela vizinhança a é toda absorvida pelo corpo negro.
Substituindo e na equação de :
Agora é só somar e pra achar .
Essa é a letra (d) da questão! Ou seja, a resposta certa é a letra (d)!
Resposta
Letra (d)
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 104-2-102
Uma esfera com de diâmetro cuja superfície é mantida à temperatura de é suspensa no meio de uma sala a . Considerando que o coeficiente de transferência de calor por convecção é de e a emissividade da superfície corresponde , determine a taxa total de transferência de calor da esfera.
Passo 1
Oi, chuchus, pront@s pra essa questão que mistura convecção com radiação?
O enunciado pede para a gente calcular a taxa de calor que a superfície de uma esfera perde de duas formas. Uma parte de , que chamaremos de , é perdida por convecção. Essa parte é calculada com a lei de resfriamento de Newton abaixo.
onde é o coeficiente de transferência de calor por convecção de , é a área da superfície esférica com diâmetro de , é a temperatura da superfície que vale e é a temperatura do ar a .
A outra parte de é perdida por radiação e é calculada abaixo:
Essa fórmula mostra que, pra gente calcular a parcela que a superfície perde por radiação, temos que calcular a quantidade que ela perde por emitir radiação menos a quantidade que ela ganha por absorver radiação das superfícies ao redor! Essas duas taxas são calculadas através da lei de Stefan-Boltzmann. A figura abaixo mostra melhor o problema.
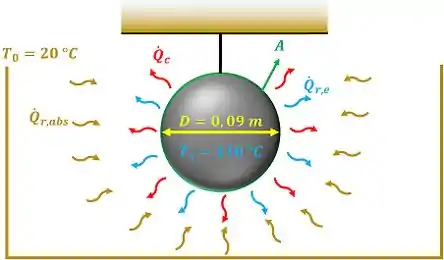
Com essas informações, vamos iniciar as contas no passo seguinte!
Passo 2
Vamos iniciar as contas, calculando a taxa de calor que a superfície perde por convecção.
Fazemos isso, substituindo os dados que temos na fórmula de do passo 1.
No entanto, antes precisamos calcular a área da superfície esférica através da equação abaixo.
Agora sim podemos substituir os dados.
No próximo passo calcularemos !
Passo 3
Pra calcular a parcela de taxa de calor que a superfície perde por radiação, temos que achar a taxa que ela emite por radiação. A equação abaixo calcula esse valor.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície. O enunciado informou que o valor dessa emissividade vale ! Para achar só falta converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Agora só falta achar pra calcular e !
Passo 4
Para calcular a taxa de calor por radiação que o corpo esférico absorve, temos que saber que um corpo com emissividade de absorve das radiações que chegam até ele por todos os lados. Logo, da radiação emitida pela vizinhança a é absorvida pela esfera.
Substituindo e na equação de :
Agora é só somar e pra achar .
Acabooooou! Encontramos o resultado que o enunciado pediu!
Resposta
Exercício Resolvido #6
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 68-2.55
A superfície externa da grelha com cobertura mostrada na Fig. P2.55 está a e sua emissividade corresponde a . O coeficiente de transferência de calor por convecção entre a grelha e a vizinhança é . Determine a taxa líquida de transferência de calor entre a grelha e a vizinhança por convecção e radiação , em por de área de superfície.
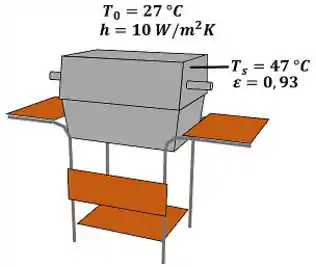
Passo 1
Fala, galera! Tudo certo pra fazer esse exercício que mistura convecção com radiação?
O enunciado pede para a gente calcular a taxa de calor por unidade de área que a superfície de uma esfera perde de duas formas. Uma parte de , que chamaremos de , é perdida por convecção. Essa parte é calculada com a lei de resfriamento de Newton.
onde é o coeficiente de transferência de calor por convecção de , é a área da superfície da grelha, é a temperatura da superfície da grelha que vale e é a temperatura do ar a .
A outra parte de é perdida por radiação e é calculada abaixo:
Essa fórmula mostra que, pra gente calcular a parcela que a superfície perde por radiação, temos que calcular a quantidade que ela perde por emitir radiação menos a quantidade que ela ganha por absorver radiação das superfícies ao redor! Essas duas taxas são calculadas através da lei de Stefan-Boltzmann. A figura abaixo mostra melhor o problema.
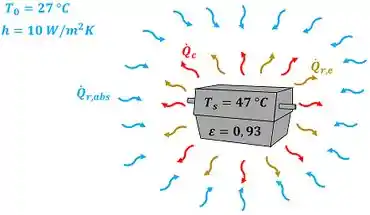
Com essas informações, vamos iniciar as contas no passo seguinte!
Passo 2
Vamos iniciar as contas, calculando a taxa de calor que a superfície perde por convecção.
Fazemos isso, substituindo os dados que temos na fórmula de do passo 1.
No próximo passo calcularemos !
Passo 3
Pra calcular a parcela de taxa de calor que a superfície perde por radiação, temos que achar a taxa que ela emite por radiação. A equação abaixo calcula esse valor.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície. O enunciado informou que o valor dessa emissividade vale ! Para achar só falta converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Agora só falta achar pra calcular e !
Passo 4
Para calcular a taxa de calor por radiação que a grelha absorve, temos que saber que um corpo com emissividade de absorve das radiações que chegam até ele por todos os lados. Logo, da radiação emitida pela vizinhança a é absorvida pela grelha.
Substituindo e na equação de :
Agora é só somar e pra achar .
Calma, porque não terminamos a questão ainda! O enunciado pedir pra gente achar o resultado em . Pra converter a unidade de pra , basta dividir a resposta por !
Agooora sim acabooooou! Encontramos o resultado que o enunciado pediu na unidade certa!
Resposta
Exercício Resolvido #7
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 68-2.54
Um corpo cuja área superficial é , emissividade é e temperatura é é colocado em uma grande câmara de vácuo, cujas paredes estão a . Qual a taxa de radiação emitida pela superfície em ? Qual é a taxa líquida de radiação trocada entre a superfície e as paredes da câmara, em ?
Passo 1
Então, gente, esse é um exercício de radiação que pede duas informações. Primeiro, a questão pede o valor da taxa de calor que um corpo emite por radiação. Depois, ela pede o valor da taxa de calor que o corpo e a câmara trocam por radiação! Essa taxa de calor é igual à taxa que o corpo emite, menos a taxa que ele absorve de radiação da câmara.
A figura abaixo mostra os dados que temos pra calcular .
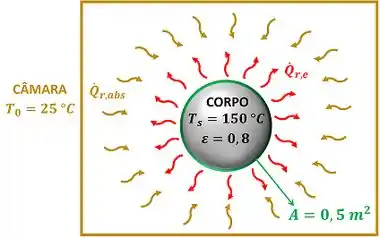
é a área do corpo, é a temperatura da superfície do corpo, é a temperatura da câmara e é a emissividade do corpo.
Pra calcular e , usaremos a lei de Stefan-Boltzmann.
Sabendo de tudo isso, podemos partir pro próximo passo que é calcular .
Passo 2
Como dito, calculamos a taxa de calor emitido por radiação pelo corpo através da lei de Stefan-Boltzmann abaixo.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície. O enunciado informou que o valor dessa emissividade vale ! Para achar temos que converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Obaaaa! Já achamos a primeira informação que o enunciado pediu pra gente!
Agora só falta achar pra calcular !
Passo 3
Para calcular a taxa de calor por radiação que o corpo absorve, temos que saber que um corpo com emissividade de absorve das radiações que chegam até ele por todos os lados. Logo, da radiação emitida pela vizinhança a é absorvida pelo corpo.
Substituindo e na equação de :
Uhuuuul! Achamos a segunda informação que o enunciado nos pediu e acabamos a questão!
Resposta
Exercício Resolvido #8
Elaboração própria
Uma esfera com de diâmetro cuja superfície é mantida à temperatura de é suspensa no meio de uma sala a por . Considerando que o coeficiente de transferência de calor por convecção é de e a emissividade da superfície corresponde , determine a perda de calor total da esfera.
Passo 1
Fala, pessoal! O enunciado pede para a gente calcular o calor que a superfície de uma esfera perde de duas formas. Uma parte de , que chamaremos de , é perdida por convecção. A outra parte de é perdida por radiação.
e são calculadas, multiplicando a taxa de perda de calor por convecção e a taxa de perda de calor por radiação pelo quantidade de tempo durante a qual a esfera troca com o ambiente.
A taxa de calor perdida é encontrada através da lei de resfriamento de Newton abaixo.
onde é o coeficiente de transferência de calor por convecção de , é a área da superfície esférica com diâmetro de , é a temperatura da superfície que vale e é a temperatura do ar a .
é calculada abaixo:
Essa fórmula mostra que, pra gente calcular a taxa de calor perdida por radiação, temos que calcular a quantidade que a superfície perde por emitir radiação menos a quantidade que ela ganha por absorver radiação das superfícies ao redor! Essas duas taxas são calculadas através da lei de Stefan-Boltzmann. A figura abaixo mostra melhor o problema.
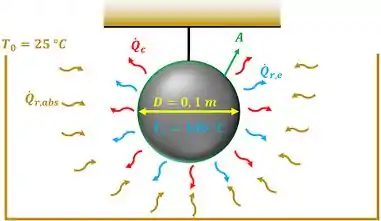
Com essas informações, vamos iniciar as contas no passo seguinte!
Passo 2
Vamos iniciar as contas, calculando a taxa de calor que a superfície perde por convecção.
Fazemos isso, substituindo os dados que temos na fórmula de do passo 1.
No entanto, antes precisamos calcular a área da superfície esférica através da equação abaixo.
Agora sim podemos substituir os dados.
Agora, multiplicamos por pra achar . Antes, temos que converter a unidade da quantidade de tempo que o ar da sala e a esfera trocam calor de horas pra segundos. Fazemos isso, multiplicando por .
No próximo passo calcularemos e !
Passo 3
Pra calcular a parcela de taxa de calor que a superfície perde por radiação, temos que achar a taxa que ela emite por radiação. A equação abaixo calcula esse valor.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície. O enunciado informou que o valor dessa emissividade vale ! Para achar só falta converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Para calcular a taxa de calor por radiação que o corpo esférico absorve, temos que saber que um corpo com emissividade de absorve das radiações que chegam até ele por todos os lados. Logo, da radiação emitida pela vizinhança a é absorvida pela esfera.
Com esse valores, somos capazes de achar e no próximo passo!
Passo 4
Substituindo e na equação de :
Multiplicando essa taxa de calor perdida por radiação por , encontramos .
Agora é só somar e pra achar .
Fechamos o exercício, pessoal! Parabéns pra nós!