Exercícios Resolvidos de Teste de Hipótese para Média Amostral com σ Desconhecido
Ver TeoriaEnunciado
Teste de Hipóteses
Em um determinado shopping do Rio de Janeiro, queremos saber se os gastos médios de duas lojas com o mesmo perfil, podem ser considerados estatisticamente idênticos.
Tomou-se uma amostra de clientes da loja e de clientes da loja , obteve as seguintes estimativas:
Testar a hipótese se existe diferença entre a média dos gastos da loja e a média dos gastos da loja , ao nível de significância de .
Mostre este resultado através de cálculo e esboce um gráfico da distribuição do teste indicando a área de rejeição e aceitação.
Passo 1
Primeiro vamos anotar de novo os dados de cada amostra...
O exercício pede pra gente testar a hipótese de existir ou não diferença entre as médias verdadeiras dos gastos das duas lojas... nosso teste vai ter as seguintes hipóteses então:
Concorda? Não importa se um for maior ou menor que o outro, só quero saber se são iguais ou diferentes.
Esse teste é daquele caso que a gente viu.
Passo 2
Já que a gente já montou o teste, vamos fazer a nossa estatística de teste, que nesse caso de diferença entre médias quando a gente não conhece os desvios padrões e , é:
Sendo que se a gente tá testando a hipótese das médias serem iguais , então , concorda? Fica assim...
Com:
Assustador, não? Mas é só conta, fica calmo.
Substituindo os valores... dá uma olhadinha ali em cima, a gente já conhece todos!
E:
Passo 3
Pra fechar a gente precisa saber a região crítica do nosso teste, e ver se estamos fora ou dentro dessa região.
Pra esse teste (caso ), a região crítica é:
Usamos já que a gente não conhece os desvios padrões nominais.
Maaaas, tem um porém dessa vez.. o número de graus de liberdade que a gente tem nesse exercício é:
Como temos grau de liberdade maior do que , podemos usar a Normal no lugar do .
A região crítica vai ser então...
Passo 4
Pra nível de significância de ...
Usei o valor da tabela mais aproximado.
Passo 5
Nossa região crítica fica sendo:
E a nossa estatística de teste deu:
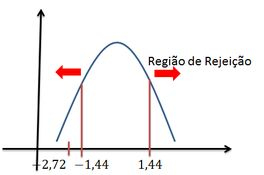
Estamos dentro da região crítica (ou de rejeição), então rejeitamos ao nível de significância de .
O esboço fica assim:
