Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Testes Lógicos (If, Else, Elseif e Switch Case)

Ver Teoria
Exercício 51234678

Enunciado

Dada que uma equação de segundo grau pode ser representada da seguinte forma:

A X 2 + B X + C = 0

Utilizando as equações de Bhaskara, crie um algoritmo e escreva um programa que calcule as raízes REAIS da equação de segundo grau, e se caso a raiz for complexa cancelar o cálculo informando que a raiz é complexa.

Passo 1

A questão pede que a gente crie um algoritmo e um programa que calcule as raízes reais da função de segundo grau.

Se as raízes forem complexas, deve-se parar o cálculo revelando que a raiz é complexa.

Lembrando que para achar as soluções da equação de segundo grau, precisamos de duas equações, uma delas é o discriminante ∆ e outra que é a equação de Bhaskara.

∆ = B 2 - 4 A C

X = - B ± ∆ 2 A

Como temos uma raiz do discriminante, é ele que vai dizer o tipo de solução que nossa equação de segundo grau tem:

  • Se ∆ < 0 , então nossas raízes X não serão reais.

E tudo será definido em função dos coeficientes a , b e c da equação!

Ah essa questão tem diversas formas de programar, cada um faz do jeito que achar melhor meu jeito não é o absoluto. Porém ao testar com os mesmo coeficientes que os meus, você tem que achar o mesmo valor.

Passo 2

Primeiramente, para responder à questão precisamos elaborar o algoritmo!

Para que a equação tenha raízes REAIS, o discriminante precisa ser maior do que 0. Pois se for menor do que 0 a raiz será complexa e o cálculo é parado.

Então começamos calculando esse discriminante e, dependendo do seu valor, calculamos ou não o X1 e o X2.

Sendo assim o algoritmo é algo do tipo:

Passo 3

Passo 4

Uma vez que o algoritmo está pronto, precisamos agora implementar o algoritmo no Matlab.

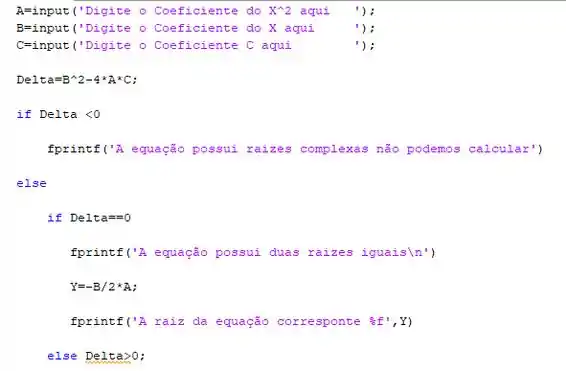
A entrada de dados fica bem assim:

A = i n p u t ( ' D i g i t e   o   C o e f i c i e n t e   d o   X ^ 2   a q u i       ' ) ;

B = i n p u t ( ' D i g i t e   o   C o e f i c i e n t e   d o   X   a q u i           ' ) ;

C = i n p u t ( ' D i g i t e   o   C o e f i c i e n t e   C   a q u i                 ' ) ;

Agora calculamos o discriminante:  

D e l t a = B ^ 2 - 4 * A * C ;

Então se o discriminante é negativo, já avisamos pro usuário que não há raízes reais:

i f   D e l t a   < 0        

        f p r i n t f ( ' A   e q u a ç ã o   p o s s u i   r a i z e s   c o m p l e x a s   n ã o   p o d e m o s   c a l c u l a r ' )

Caso contrário, ou seja, se o discriminante não é negativo, ele pode ser nulo ou positivo.

Se o discriminante é nulo, nós chamamos a raíz de Y, só pra diferenciar do caso que vai vir depois.

e l s e        

        i f   D e l t a = = 0

                              f p r i n t f ( ' A   e q u a ç ã o   p o s s u i   d u a s   r a i z e s   i g u a i s \ n ' )

                            Y = - B / 2 * A ;

                            f p r i n t f ( ' A   r a i z   d a   e q u a ç ã o   c o r r e s p o n t e   % f ' , Y )

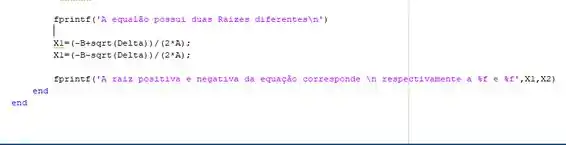
Se o discriminante é positivo, calculamos as duas raízes X1 e X2 e dizemos seus valores ao usuário.

        e l s e   D e l t a > 0 ;              

                f p r i n t f ( ' A   e q u a l ã o   p o s s u i   d u a s   R a i z e s   d i f e r e n t e s \ n ' )

                  X 1 = ( - B + s q r t ( D e l t a ) ) / ( 2 * A ) ;

                X 1 = ( - B - s q r t ( D e l t a ) ) / ( 2 * A ) ;              

                f p r i n t f ( ' A   r a i z   p o s i t i v a   e   n e g a t i v a   d a   e q u a ç ã o   c o r r e s p o n d e   \ n   r e s p e c t i v a m e n t e   a   % f   e   % f ' , X 1 , X 2 )

Precisamos ainda dar o comando end, para fechar os dois if/else que a gente abriu.

        e n d

e n d

Se digitou tudo certinho deve aparecer algo mais ou menos assim para você:

Passo 5

Utilizando A=1,B=2 e C=2 para testar o programa deverá mostrar os valores:

Resposta

Ei, a resposta está no passo a passo :)