Os dados da tabela seguinte são os da adsorção do sobre carvão a . Verifique se eles se ajustam à isoterma de Langmuir e obtenha a constante e o volume de gás correspondente ao recobrimento completo. Em cada caso, o volume foi corrigido para a pressão de .

Passo 1
Vamos arrasar nessa questão juntos! Pra começo de conversa, vamos analisar que estamos trabalhando com a adsorção de um gás, o , em um sólido, o carvão, e isso está de acordo com a adsorção de Langmuir, beleza?
Agora vamos lembrar que a isoterma de Langmuir é expressa pela equação:
Hummm… Nós precisamos encontrar a constante de Langmuir e o volume do recobrimento completo:
Bom, o enunciado nos deu um conjunto de pontos de pressão e volume, né? Aí é que tá o bizu! Se a gente plotar o gráfico versus , essa reta nos dará informações importantes, pois o coeficiente angular será e o coeficiente linear será , show!
Então vamos fazer o gráfico!!!
Passo 2
O gráfico dos nosso pontos ficará:
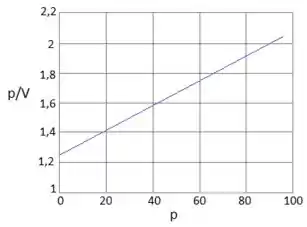
Para facilitar a visualização dos pontos vamos montar uma tabela que corresponde a esses valores:

Bom, agora só precisamos encontrar o coeficiente angular e o coeficiente linear… Para isso, vamos usar o método dos mínimos quadrados, lembra dele? Podemos fazer o método usando a calculadora científica e vamos encontrar nossos coeficientes sendo:
coeficiente angularcoeficiente linear
Passo 3
Sendo assim, temos que:
O volume de gás correspondente ao recobrimento completo, será:
Show! E agora usando o coeficiente linear, temos:
Substituindo o volume que encontramos:
O ficará:
Então, o coeficiente de Langmuir será:
Uhull!! Conseguimos!