Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Vetores e Espaço Vetorial

Ver Todos os Exercícios

Teoria

Introdução

Falaa aí! Vamos adentrar o mundo dos Espaços vetoriais agora. O nome assusta mas na prática a gente consegue seguir um roteirinho que ajuda sempre!

Vamos começar pegando a ideia desse tal espaço vetorial.

A gente consegue entender o espaço vetorial pensando em um grande conjunto V (a gente usa letras maiúsculas para nomear os espaços) com vários elementos. Os elementos desse espaço são chamados de vetores. Aqui a gente pode usar aquela velha ideia que os vetores são representados por umas flechinhas. Podemos visualizar essa ideia de conjunto com a imagem a seguir:

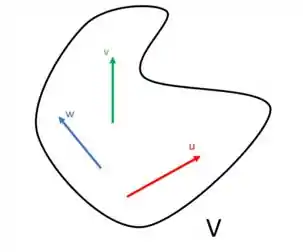
Nesta imagem, nosso espaço vetorial é o conjunto V com os vetores u, v e o w.

Apesar de eu ter dito que os vetores são representados por estas flechinhas, no mundo dos espaços vetoriais os vetores podem ser matrizes ou números também. Logo logo eu explico como que isso muda as continhas que vamos ter que fazer, ok?

Com essa ideia em mente, a gente consegue pensar em vários exemplos de espaços vetoriais. Será que um conjunto com números reais é uma espaço vetorial? Será que o conjunto das matrizes 2 × 2 é um espaço vetorial? Será que o conjunto das cores primárias é um espaço vetorial? (Endoidei? Não, a gente pode ser perguntar esse tipo de coisa)

Como responder essas perguntas? Bom, os espaços vetoriais são como uma pequena cidade que possua um xerife. Para não haver bagunça e qualquer pessoa nessa cidade faça o que quiser, existem umas leis que o xerife aplica. Quem descumprir essas regras vai ser exilado ou preso.

No espaço vetorial é a mesma coisa! A gente vai aprender aqui as regras que caracterizam um espaço vetorial e aí o xerifão vai ser você! Temos que testar todas as regras para os conjuntos que aparecerem. Se uma dessas regras não for respeitada, aquele conjunto não pode ser um espaço vetorial, ok?

Vamos agora conhecer as regras para um conjunto de vetores ser um espaço vetorial.

Regras Básicas

Aqui vamos conhecer as 3 principais regras que um conjunto V deve respeitar para ser um espaço vetorial. Algumas destas regras que eu vou mostrar aqui vão acarretar em mais outras regras. Essas regras básicas devem ser o primeiro teste que você vai realizar. Se alguma delas não for respeitada, a gente já conclui que aquele conjunto não é um espaço vetorial.

Se as 3 regras forem respeitadas, a gente vai ter que verificar algumas regrinhas a mais para concluirmos com certeza que V é um espaço vetorial, ok?

V   é um Espaço Vetorial se:

  1. V é um conjunto que contenha pelo menos um vetor;
  2. Se tivermos dois vetores u e v dentro de V , sua soma também tem que estar dentro de V ;
  3. Se pegarmos um vetor u de V e multiplicarmos por um número real qualquer, λ , o resultado deste produto tem que estar dentro de V.

Essas 3 regras que são conhecimas como os axiomas do espaço vetorial estão em uma forma traduzida, em geral, a forma que a gente usa é a seguinte:

  1. V é um conjunto não vazio;
  2. Se u , v   ∈ V → u + v   ∈ V ;
  3. Se λ ∈ R e u   ∈ V → λ . u   ∈ V .

Certinho? Beleza!

Em geral, esses 3 axiomas a gente verifica diretamente pois são mais simples de verificar. Como eu já disse antes, se nosso conjunto V obedecer esses 3 axiomas, vamos ter que verificar algumas outras regras que o nosso conjunto tem de obedecer. Tais regras vêm dos axiomas 2 e 3 que eu já mostrei ali em cima. Vamos conhece-las agora!

Propriedades do Espaço Vetorial

Outras propriedades que devemos verificar para que um conjunto V seja um espaço vetorial são apresentadas a seguir.

Para quaisquer vetores u ,   v e w pertencentes a V e a e b números reais, devemos ter:

  1. Associatividade: u + v + w = u + v + w ;
  2. Comutatividade: u + v = v + u ;
  3. Elemento Nulo: Existe um elemento 0 tal que: u + 0 = u ;
  4. Oposto: Existe um elemento - u tal que: u + - u = 0 ;
  5. Elemento Neutro: Existe um elemento 1 tal que 1 . u = u ;
  6. Associatividade: a . b . u = a . b . u ;
  7. a . u + v = a . u + a . v ;
  8. a + b . u = a . u + b . u .

Nessas propriedades, a melhor coisa a se fazer para entendermos como isso vai funcionar é partir para um exemplo. Então vamos lá!

Verificando se um conjunto é um Espaço Vetorial

Exemplo: O conjunto R 2 = { x , y /   x , y   ∈ R } é um Espaço Vetorial?

Vamos traduzir esse código aí que vai aparecer direto para a gente quando estivermos estudando esse assunto. O problema quer saber se o conjunto formado por todos os pares x , y (que são vetores com duas componentes) com x e y dois números reais quaisquer é um espaço vetorial.

Nosso trabalho de xerife da grande vila dos Espaços vetoriais começa com a tarefa de verificar se esse conjunto R 2 respeita as regras básicas. Para isso, precisamos de dois vetores quaisquer desse conjunto e um número real qualquer também. São eles:

  • u = ( x 1 , y 1 ) com x 1 e   y 1 números reais;
  • v = ( x 2 , y 2 ) com x 2 e   y 2 números reais;
  • a um número real qualquer.

    • A primeira regra básica é respeitada diretamente. Nosso conjunto é formado por qualquer par x , y com números reais, então ele nunca vai poder ser vazio. Primeiro axioma check!

    Para a segunda regra básica, temos que somar dois vetores quaisquer do nosso conjunto e ver se a soma dele está dentro do mesmo conjunto R 2 . Vamos lá:

    u + v = x 1 ,   y 1 + ( x 2 ,   y 2 )

    Para realizar essa soma, a gente soma os números que estão na mesma posição nos dois vetores. No geral, a soma é feita assim:

    x 1 ,   y 1 + x 2 ,   y 2 = ( x 1 + x 2 ,   y 1 + y 2 )

    Belezinha? Bem, como x 1 , x 2 ,   y 1 e y 2 são números reais por definição, as somas x 1 + x 2   e y 1 + y 2 resultam em dois outros números reais também. Então u + v resultou no vetor ( x 1 + x 2 ,   y 1 + y 2 ) que possui as duas componentes quaisquer dois números reais o que é exatamente o critério para estar no conjunto R 2 . Segunda regra básica, check!

    Para a terceira regra básica, temos que pegar um vetor qualquer do R 2 e multiplicar por qualquer número real a e ver se o resultado deste produto continua sendo um vetor do R 2 . Fazemos então:

    a .   u = a .   ( x 1 , y 1 )

    Para multiplicarmos um vetor por um número qualquer, a gente multiplica cada componente pelo número em questão

    a . u = a . x 1 , a . y 1

    Como x 1 e y 1 são dois números reais, o produto deles por outro número real, a , também vão ser dois outros números reais. Então a . u é um vetor com duas componentes a . x 1 e a . y 1 números reais quaisquer. Isso bate com a condição do conjunto R 2 , logo, a . u   ∈ R 2 . Terceira regra básica, check!

    As 3 regras básicas foram respeitadas. Beleeeeza pura!

    Agora temos que testar aquelas 8 propriedades. É chato fazer uma por uma, eu sei. Mas não tem jeito. Com a prática a gente acaba verificando automaticamente algumas e já ir direto naquelas que a gente suspeita que o conjunto não vai respeitar. Mas aqui, por enquanto, a gente não foge de nenhuma! Vamos lá!!

    Testando as propriedades do Espaço Vetorial

    Vamos testar cada uma das propriedades na ordem que eu listei agora há pouco. Caso alguma das propriedades seja quebrada, a gente já para nessa propriedade e já diz que o conjunto não é um espaço vetorial, ok?

    Também vamos usar aqui

  • u = ( x 1 , y 1 ) com x 1 e   y 1 números reais;
  • v = ( x 2 , y 2 ) com x 2 e   y 2 números reais;
  • w = ( x 3 , y 3 ) com x 3 e   y 3 números reais;
  • a ,   b e c sendo números reais quaisquer.

Partiu verificar as propriedades!

Primeira propriedade: Começamos calculando o lado esquerdo da igualdade

u + v + w = x 1 , y 1 + x 2 ,   y 2 + x 3 , y 3 somando os dois vetores que estão dentro dos parêntesis, temos:

( u + v ) + w = ( x 1 + x 2 , y 1 + y 2 ) + x 3 , y 3

Somando os dois vetores que restaram:

u + v + w =   x 1 + x 2 + x 3 , y 1 + y 2 +   y 3

Vamos agora calcular o lado direito da propriedade e ver se o resultado bate com o que obtivemos aqui em cima:

u + v + w = x 1 ,   y 1 + x 2 , y 2 + x 3 ,   y 3 u + v + w = x 1 , y 1 + x 2 + x 3 ,   y 2 + y 3 u + v + w = x 1 + x 2 + x 3 , y 1 + y 2 + y 3

Como os dois resultados deram exatamente iguais, concluímos que:

u + v +   w = u + v + w

E a primeira propriedade está OK! Vamos para a próxima!

Segunda propriedade: Começamos calculando o lado esquerdo da igualdade:

u + v = x 1 ,   y 1 + x 2 ,   y 2 = x 1 + x 2 ,   y 1 + y 2

Calculando o lado direito dessa propriedade:

v + u =   x 2 ,   y 2 + x 1 ,   y 1 = x 2 + x 1 ,   y 2 + y 1

Como x 1 , x 2 , y 1 e y 2 são todos reais, eles respeitam a comutatividade, então:

x 2 + x 1 = x 1 + x 2 y 2 + y 1 = y 1 + y 2

Substituindo isso no resultado de v + u , temos: v + u =   x 1 + x 2 ,   y 1 + y 2  

Então, comparando os dois resultados, vemos que:

u + v = v + u

Segunda propriedade, OK! Próxima!!

Terceira propriedade: Vamos começar verificando se o elemento nulo está presente nesse conjunto. Como estamos falando do R 2 o elemento nulo neste espaço é um vetor com as duas componentes nulas: 0 = ( 0,0 )

Como o nosso exemplo nos deu um conjunto de todos os possíveis pares x , y desde que x e y sejam reais, podemos escolher x = 0 e y = 0 e o nosso vetor vai ser o vetor nulo. Então, esse conjunto possui o vetor nulo 0 = ( 0,0 ) .

Agora vamos somar qualquer vetor, u , com esse vetor nulo e ver se a segunda propriedade bate: u + 0 = x 1 , y 1 + 0,0 = ( x 1 + 0 ,   y 1 + 0 )

Realizando a soma, obtemos

u + 0 = x 1 , y 1 = u

Terceira propriedade, OK! Vamos para a quarta!

Quarta propriedade: Precisamos ver se para qualquer vetor de R 2 (vou escolher o u ) a soma com o vetor - u que é dado por

- u =   - x 1 ,   y 1 = - x 1 ,   - y 1

resulta no vetor no nulo.

Vamos calcular, então:

u + - u = x 1 , y 1 + - x 1 ,   - y 1 u + - u = x 1 + - x 1 ,   y 1 + - y 1

Como + com – dá - , temos:

u + - u = x 1 - x 1 ,   y 1 - y 1 = 0,0 = 0

OK! A soma do vetor com seu oposto resulta no vetor nulo. Quarta propriedade, OK! Vamos para a quinta.

Quinta propriedade: Temos que ver se existe algum número real que se multiplicarmos ele pelo nosso vetor, continuamos com o mesmo vetor. Bem, se escolhermos o número 1 mesmo, teremos:

1 .   u = 1 . x 1 ,   1 . y 1 = ( x 1 ,   y 1 )

Desta maneira, concluímos que:

1 . u = u

Quinta propriedade, check! Vem para nós, sexta!!

Sexta propriedade: Vamos começar calculando o lado esquerdo da propriedade, depois a gente calcula o direito e vemos se as respostas batem. Vamos lá:

a . b . u = a .   b .   x 1 ,   y 1 = a .   b . x 1 ,   b . y 1 a . b . u = a . b . x 1 ,   a . b . y 1

Calculando o lado direito, temos:

a . b . u = a . b . x 1 ,   y 1 = a . b . x 1 ,   a . b . y 1 a . b . u = ( a . b . x 1 ,   a . b . y 1 )

Comparando os dois resultados, podemos dizer que

a . b . u = a . b . u

Sexta propriedade, ok também. Próxima!!

Sétima propriedade: Vamos começar calculando o lado esquerdo da propriedade, depois a gente calcula o direito e vemos se as respostas batem. Vamos lá:

a .   u + v = a .   ( x 1 + x 2 ,   y 1 + y 2 )

Aqui eu já usei o resultado de u + v que já calculamos anteriormente. Realizando o produto, temos

a .   u + v = a .   x 1 + x 2 ,   a .   y 1 + y 2 =   ( a . x 1 + a . x 2 ,   a . y 1 + a . y 2 )  

Beleza, vamos calcular o lado direito agora:

a . u + a . v = a . x 1 ,   a . y 1 +   a . x 2 ,   a . y 2 =   ( a . x 1 + a . x 2 ,   a . y 1 + a . y 2 )  

Comparando os dois resultados, podemos afirmar que

a .   u + v = a . u + a . v  

Shoow! Vamos para a última propriedade. A última esperança desse conjunto ser um Espaço Vetorial. Partiu!

  1. a + b . u = a . u + b . u .

Oitava propriedade: Vamos começar calculando o lado esquerdo da propriedade, depois a gente calcula o direito e vemos se as respostas batem. Vamos lá:

a + b . u = a + b . x 1 ,   a + b . y 1

Podemos fazer uma distributiva ali:

a + b . u = a . x 1 + b . x 1 ,   a . y 1 + b . y 1

Calculando o lado esquerdo da propriedade:

a . u + b . u = a . x 1 ,   a . y 1 +   b . x 1 ,   b . y 1 =   a . x 1 + b . x 1 ,   a . y 1 + b . y 1  

Comparando os dois resultados, podemos concluir que:

a + b . u =   a . u + b . u  

Opa! A última propriedade também confere!! Como todas as propriedades batem, podemos dizer com toda a certeza que o conjunto dado, o R 2 , é um Espaço Vetorial!!

Shooow! Esse procedimento vai valer sempre, testaremos sempre as propriedades nos conjuntos que forem aparecendo. Porém, cada conjunto vai ter sua particulariedade então não tem jeito, vamos afiar esses dedos aí resolvendo uns exercícios? Partiiiiiiiu 😊

Propriedades do Espaço Vetorial

Verificando se um conjunto é um Espaço Vetorial

Testando as propriedades do Espaço Vetorial

Exercícios Resolvidos

Exercício Resolvido #1

Apostila Álgebra Linear - UFF

Determine as componentes do vetor v = P 1 P 2 → de ponto inicial P 1 2 ,   - 1 e ponto final P 2 7 ,   5 .

Passo 1

Faaaala galerinhaa !! Prontos para começar mais uma questão?!

Beleza, nossa questão pede pra gente achar as componentes do vetor que vai do ponto P 1 ao ponto P 2 . Então vamos primeiro entender o que é um vetor.

Bom, os vetores são aqueles segmentos de reta que possuem um certo “tamanho” e “apontam” para um certo ponto, ou seja, possuem direção e sentido !!

Aqui na álgebra os vetores deve sair da origem e chegar até o ponto de interesse, certo? Mas nem sempre isso acontece !!

Muitas vezes, como aqui, o vetor sai de um ponto P 1 e vai para P 2 . Como na figura:

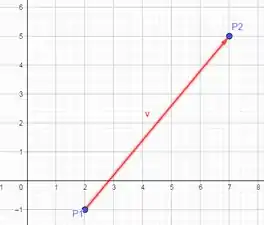
Para achar o vetor v vamos começar traçando um vetor que vamos chamar de u , que vai da origem até P 1 , e outro que chamaremos de w , que vai da origem até P 2 :

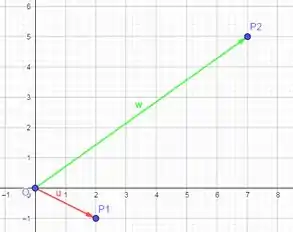
E agora? Como faremos para achar o vetor v propriamente dito?

Pra isso, basta fazermos uma subtração de vetores. Como queremos que v saia de P 1 e chegue em P 2 , temos que fazer o vetor final menos o vetor inicial:

v = P 2 - P 1

v = w - u

A ordem certa é muito importante, pois é ela quem vai indicar o sentido do nosso vetor. Se trocarmos a ordem dos vetores na subtração, o vetor resultante vai ficar apontando no sentido contrário e ficará errado. Então, bastante atenção na ordem, ok!

Passo 2

Então galerinha, pra fazer essa subtração vamos lembrar que os vetores podem ser escritos como matriz coluna, ou seja:

P 1 = 2 ,   - 1 → u = 2 - 1

P 2 = ( 7,5 ) → w = 7 5

Como nossos pontos P 1 e P 2 têm coordenadas x e y ! Então, temos vetores no espaço bidimensional, R 2 !

Colocando na subtração:

v = w - u

7 5 - 2 - 1

Para fazer a subtração entre essas matrizes, temos que subtrair os elementos que estão na mesma posição das duas matrizes.

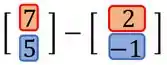
Subtraimos o primeiro termo de w lá do primeiro termo de u e assim por diante!

v = 7 - 2 5 + 1 = 5 6

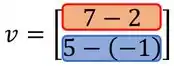
Encontramos as coordenadas do nosso vetor resultante:

v = 5 6

Tranquilinho, não foi ?!

Bora seguir?

Resposta

v = 5 6

Exercício Resolvido #2

Apostila Álgebra Linear - UFABC

Se v → = 1 , - 2,3 , determine 3 v → .

Passo 1

Mais uma questão pra gente ficar craque em vetores e suas manipulações!!

Nela, o que nós teremos que fazer é determinar o triplo do vetor, já que ele pediu pra gente descobrir quem é 3 v → .

Vamos começar desenhando este vetor?

Em álgebra podemos representar os vetores saindo da origem ( 0,0 , 0 ) e indo até um certo ponto, P 1 , - 2,3 que possui as mesmas coordenadas do vetor. No nosso caso nós chamamos este vetor de v → !

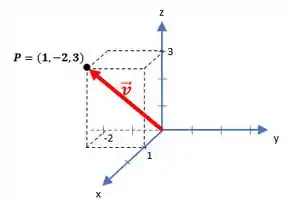
Então, como os vetores podem ser escritos como matriz coluna, nosso vetor se transforma em:

v = 1 - 2 3

Onde o primeiro elemento indica a coordenada o x , o segundo a coordenada y e o terceiro a coordenada z ! Então, temos um vetor no espaço tridimensional, R 3 !

Pra encontrar o triplo deste vetor, vamos fazer a multiplicação dele por 3 :

3 v = 3 × 1 - 2 3

Como estamos multiplicando um número real por uma matriz, este 3 vai multiplicar cada elemento da matriz coluna, como se fosse uma grande distributiva:

3 v = 3 × 1 3 × ( - 2 ) 3 × 3

Resolvendo as multiplicações, teremos:

3 v = 3 - 6 9

Vamos desenhar pra ver como agora este vetor está três vezes maior?

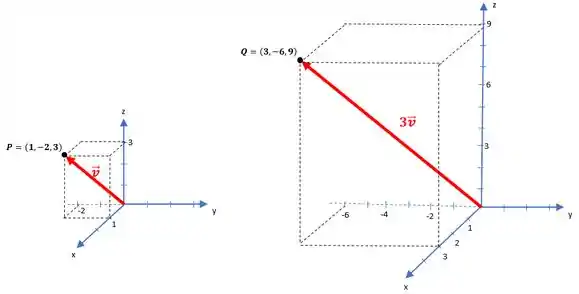
Muita diferença, não é? O que a gente pode perceber também é que na multiplicação por 3, só o que mudou foi o tamanho do vetor, mas ele continua com a mesma direção e o mesmo sentido!

E com isso encontramos nossa resposta.

Resposta

3 v = 3 - 6 9

Exercício Resolvido #3

Apostila Álgebra Linear - UFABC

Se V 1 , - 2 ,   3 e W = ( 2 ,   4 ,   - 1 ) , determine V + W .

Passo 1

Mais uma pra nossa seção, ein?!

O que o exercício está querendo é que a gente faça a soma entre esses dois vetores, então vamos lá!

Os vetores sempre podem ser escritos na forma matricial. Pra isso, nós construímos uma matriz coluna com cada linha correspondendo a uma coordenada do nosso vetor.

Então vamos fazer isso?

V = 1 - 2 3

W = 2 4 - 1

Agora vamos realizar a soma dessas matrizes que acabamos de encontra.

Colocando na soma:

V + W

1 - 2 3 + 2 4 - 1

Para somar duas matrizes, somamos os elementos que ocupam as mesmas posições. Ou seja, o primeiro elemento de uma coluna com o primeiro da outra, e assim sucessivamente:

V + W = 3 2 2

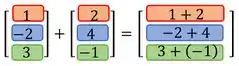
E assim encontramos a soma que estávamos procurando.

Resposta

V + W = 3 2 2

Exercício Resolvido #4

Apostila Álgebra Linear - UFF

Sejam u   4 ,   - 1 , v   0,5 e w = - 3 , - 3 . Encontre 3 v - 2 u + 2 w .

Passo 1

Show galerinha, nessa questão nós temos mais operações a serem feitas, mas o procedimento é o mesmo!!

Primeiro de tudo, vamos colocar os vetores na forma matricial. Pra isso, nós construímos uma matriz coluna com cada linha correspondendo a uma coordenada do nosso vetor. Assim teremos as matrizes:

u = 4 - 1

v = 0 5

w = - 3 - 3

Beleza, agora vamos começar a resolver.

Passo 2

A questão está querendo que a gente faça:

3 v - 2 u + 2 w

Mas antes de substituir as matrizes que encontramos nessa expressão, vamos organizá-la um pouquinho! Podemos ver que o 2 está multiplicando o que está dentro dos parênteses, então vamos resolver essa multiplicação fazendo uma distributiva:

3 v - 2 u - 4 w

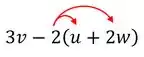
Agora sim, vamos substituir as matrizes correspondentes aos vetores v , u e w nessa expressão:

3 v - 2 u - 4 w

3 × 0 5 - 2 × 4 - 1 - 4 × - 3 - 3

Multiplicamos cada elemento da matriz pelo que está de fora:

3 × 0 3 × 5 - 2 × 4 2 × ( - 1 ) - 4 × ( - 3 ) 4 × ( - 3 )

E teremos:

= 0 15 - 8 - 2 - - 12 - 12

Agora, o que nos resta é realizamos as operações. Como são subtrações, podemos criar uma nova matriz resultante onde os elementos serão o resultado das operações realizadas com os elementos que estavam na mesma posição:

Resolvendo as operações de cada linha, encontramos nossa resposta:

3 v - 2 u - 4 w = 4 29

Legal, não foi?

Resposta

3 v - 2 u - 4 w = 4 29

Exercício Resolvido #5

Apostila Álgebra Linear - UFF

Determine as componentes do vetor V que tem um representante com ponto inicial P 5 2 ,   1 ,   2 e ponto final Q 0 , 5 2 , 5 2 .

Passo 1

Vamos para mais uma meus queridos?!

Aqui na álgebra os vetores devem sair da origem e chegar até o ponto de interesse, certo? Mas nem sempre isso acontece!!

Muitas vezes, como aqui, o vetor sai de um ponto P e vai para Q , e nós escrevemos como:

V = P Q →

E agora?

Como faremos para achar o vetor V propriamente dito?

Basta fazermos uma subtração de vetores:

v = Q - P

Mas Atenção! Aqui temos que ter cuidado com a ordem, vamos fazer o ponto final menos o inicial. Se trocarmos a ordem, nosso vetor ficará representado com sentido contrário, se tornando outro vetor, diferente do que a gente estava procurando.

Passo 2

Então galerinha, os vetores podem ser escritos como matriz coluna, ou seja:

P = 5 2 1 2

Q = 0 5 2 5 2

Onde o primeiro elemento da matriz indica a coordenada x , o segundo a coordenada y e o terceiro a coordenada z ! Então, temos um vetor no espaço tridimensional, R 3 !

Colocando na subtração:

V = 0 5 2 5 2 - 5 2 1 2

Para resolver nós precisamos subtrair o primeiro elemento da matriz coluna P lá do primeiro elemento de Q , e assim por diante!

V = 0 - 5 2 5 2 - 1 5 2 - 2

Como temos subtrações com frações aí no meio das operações, temos que colocar os números no mesmo denominador. Pra isso, colocamos o 1 embaixo dos números inteiros e multiplicamos em cima e embaixo pelo denominador da fração que estiver sendo calculada com ele.

V = 0 1 - 5 2 5 2 - 1 1 5 2 - 2 1

V = 0 1 × 2 2 - 5 2 5 2 - 1 1 × 2 2 5 2 - 2 1 × 2 2

V = 0 2 - 5 2 5 2 - 2 2 5 2 - 4 2

Agora que já estão com o mesmo denominador, podemos resolver em cima e repetir embaixo, ficando com:

V = - 5 2 3 2 1 2

E por fim, encontramos nossa resposta. Bora seguir?

Resposta

V = - 5 2 3 2 1 2

Exercício Resolvido #6

Apostila Álgebra Linear - UFABC

Determine a norma do vetor V = 1 ,   - 2 ,   3 .

Passo 1

Preparados para mais uma?

Bom galera, o exercício pede pra gente determinar a norma o vetor. Então precisamos saber que a norma é o comprimento que o vetor apresenta, certo?

Pensando dessa forma, a norma nos mostra qual é a distância entre dois pontos, o ponto inicial e o ponto final do vetor!!

Aqui na álgebra os vetores devem sair da origem e chegar até o ponto de interesse. No caso de V , a norma será a distância da origem até o ponto final de V , que é o ponto que possui as mesmas coordenadas do V .

Para calcular a distância entre dois pontos, e consequentemente a norma do vetor que os liga, podemos usar a fórmula:

V = x 2 + y 2 + z 2

Essas barrinhas duplas aplicadas a um vetor significam exatamente a norma desse vetor, ok?

Então, como nosso vetor tem coordenadas:

x = 1

y = - 2

z = 3

Colocando na fórmula da norma:

V = 1 2 + - 2 2 + 3 2

Um detalhe que não podemos deixar passar é que qualquer número ao quadrado será sempre positivo. Então aquele - 2 2 vai dar + 4 , beleza?

V = 1 + 4 + 9

V = 14

Como não há raiz inteira do número 14 , podemos deixar nossa reposta dessa forma. E concluímos que esse vetor ter comprimento igual a 14 .

E é simples assim, gostaram?!

Resposta

V = 14

Exercício Resolvido #7

Apostila Álgebra Linear - UFABC

Ache a distância entre os pontos P = 2 ,   - 3 ,   1 e Q = - 1 ,   4 ,   5 .

Passo 1

Vamos que vamos?!

Boa galera, a norma representa a distância entre dois pontos, neste caso P e Q !

Quando o vetor vai da origem até um ponto qualquer, a norma é simplesmente:

V = x 2 + y 2 + z 2

Agora, quando o vetor não parte da origem 0 ,   0 ,   0 , mas sim de outro ponto conhecido, podemos escrever a norma como a distância entre esses dois pontos. Para isso faremos:

V = x Q - x P 2 + y Q - y P 2 + z Q - z P 2

Então, vamos separar as coordenadas de cada vetor. olhando os vetores P e Q , temos:

P = 2 ,   - 3 ,   1

x P = 2

y P = - 3

z P = 1

E Q = - 1 ,   4 ,   5

x Q = - 1

y Q = 4

z Q = 5

Agora, colocando na fórmula da norma:

V = x Q - x P 2 + y Q - y P 2 + z Q - z P 2

V = - 1 - 2 2 + 4 - - 3 2 + 5 - 1 2

Vamos resolver os parênteses primeiro:

V = - 3 2 + 7 2 + 4 2

Agora elevamos cada um ao quadrado:

V = 9 + 49 + 16

E por fim, fazemos a soma:

V = 74

E assim chegamos a nossa resposta final. Então a distância entre os pontos P e Q é igual a 74 .

Resposta

V = 74

Exercício Resolvido #8

Apostila Álgebra Linear - UFABC

Ache o vetor unitário na direção do vetor V = 1 ,   - 2 ,   3 .

Passo 1

Vamos para mais uma bem legal?

Bom galera, um vetor unitário é um vetor que possui norma igual a 1 !! Ou seja, ele tem uma unidade de comprimento. E aponta na mesma direção e sentido do vetor que estamos calculando.

Estes vetores são bem importantes para especificar a direção de uma grandeza vetorial, por exemplo.

Shoow!!

Então, vamos ver como determinamos o vetor unitário. Pra isso vamos chamar ele de u . E fazer:

u = 1 V V

Para encontrar u , a primeira coisa a ser feita é achar a norma do nosso vetor V , que é esse V .

Passo 2

Como aqui na álgebra os vetores devem sair da origem e chegar até o ponto de interesse, formando o vetor V ,     então a norma será dada pelo comprimento de V .

Que é expressa por:

V = x 2 + y 2 + z 2

Então, olhando no vetor:

V = 1 ,   - 2 ,   3

Temos:

x = 1

y = - 2

z = 3

Colocando na fórmula da norma:

V = 1 2 + - 2 2 + 3 2

V = 1 + 4 + 9

E assim teremos a norma do vetor V

V = 14

Passo 3

E agora aplicamos essa norma na fórmula do vetor unitário:

u = 1 V V

u = 1 14 ∙ ( 1 , - 2,3 )

Veja que precisamos fazer a multiplicação de um vetor por um número real, que é esse 1 14 que está ali na frente do vetor.

Com isso, multiplicamos cada coordenada do vetor pelo 1 14 , e teremos:

u = 1 14 ,   - 2 14 , 3 14

E assim encontramos nosso vetor unitário, gostaram?!

Resposta

1 14 ,   - 2 14 , 3 14

Exercício Resolvido #9

Apostila Álgebra Linear - UFABC

Ache o produto escalar de V = 0 ,   1 ,   0 e W = 2 ,   2 ,   3

Passo 1

Bom galerinha, o produto escalar entre dois vetores é calculado simplesmente pela soma da multiplicação dos termos correspondentes de cada vetor!

E desde agora, já é bom a gente ter em mente que quando falamos em produto escalar, o nosso resultado precisa ser um escalar, o que é na verdade um número e não um vetor. Isso ajudará a gente a não fazer confusão com outros produtos que podem ser feitos entre vetores.

Também vamos usar os símbolos de multiplicação que é o pontinho entre os dois vetores. Isso indicará que é um produto escalar.

Vamos ver como fica nosso produto escalar para vetores genéricos:

V = v 1 ,   v 2 ,   v 3

W = w 1 ,   w 2 ,   w 3

Temos de multiplicar o primeiro termo do vetor V com o primeiro termo do vetor W . O segundo com o segundo e assim por diante, e depois somar essas multiplicações. Multiplicando teremos:

V ∙ W = v 1 w 1 + v 2 w 2 + v 3 w 3

Agora que nós já pegamos o processo, bora resolver para os nossos vetores V e W ?

Sendo V = 0 ,   1 ,   0 e W = 2 ,   2 ,   3

V ∙ W = 0 ,   1 ,   0 ∙ 2 ,   2 ,   3

= 0 ∙ 2 + 1 ∙ 2 + 0 ∙ 3

V ∙ W = 0 + 2 + 0

V ∙ W = 2

E assim aparece nosso escalar, não disse que daria um número no final?!

Resposta

V ∙ W = 2

Exercício Resolvido #10

Apostila Álgebra Linear - UFF

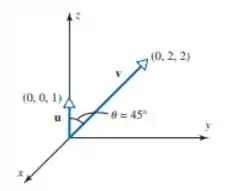
Encontre o produto escalar entre os vetores u e v , mostrados na Figura :

Passo 1

E para fechar com chave de ouro vamos fazer mais uma!!

O produto escalar entre dois vetores pode ser calculado como:

V ∙ U = v 1 u 1 + v 2 u 2 + v 3 u 3

Mas, no nosso caso, temos o ângulo de 45° ali. Então o produto escalar pode ser calculado levando em consideração esse ângulo, através da expressão:

V ∙ U = V U . cos ⁡ θ

Veja que devemos fazer o módulo de um, vezes o módulo do outro, vezes o cosseno do ângulo entre eles.

Vamos começar lembrando a fórmula do módulo?

V = v 1 2 + v 2 2 + v 3 2

U = u 1 2 + u 2 2 + u 3 2

  • Para V = 0,2 , 2

    • Substituindo:

    V = 0 2 + 2 2 + 2 2 =

    4 + 4 = 8

    Podemos simplificar a raiz de oito, lembrando que 8 = 2.2 . 2 = 2 2 . 2

    2 2 . 2

    Com isso, o 2 2 que está dentro da raiz, pode sair da raiz, ficando:

    = 2 2

    E esse é o módulo de V

  • Agora vamos fazer o módulo de U = 0,0 , 1

U = 0 2 + 0 2 + 1 2

= 1 = 1

Passo 2

Agora vamos colocar tudo que descobrimos na expressão do produto escalar.

Se o ângulo entre os vetores é 45 ° :

V ∙ U = V U . cos ⁡ θ

V ∙ U = 2 2 1 . cos ⁡ 45 °

Aqui precisaremos substituir o cosseno de 45 ° , que vale 1 2

Ficando com:

V ∙ U = 2 2 . 1 .

Note que temos 2 multiplicando e dividindo, então vamos cortar, ficando só com:

V ∙ U = 2

E assim, encontramos nosso produto escalar!

Passo 3

Que tal fazer o teste com a outra fórmula só para ver no que dá?

V ∙ U = ( 0,2 , 2 ) ∙ ( 0,0 , 1 )

= 2 ∙ 0 + 2 ∙ 0 + 2 ∙ 1

V ∙ U = 2

Igualzinho, não é?

Então vocês podem usar as duas formas, cabe a você avaliar qual será melhor para cada situação!!

E assim nós chegamos ao fim de mais uma seção!!

Resposta

V ∙ U = 2

Exercícios de Livros Relacionados

(a) S = {O, (1/ √2, −1/√2), (1/√2, 1/√2)} e P = (1, 3);