Considere a função definida com matrizes de tamanho por , sendo
Esboce juntamente com em cada caso dado. Como você descreveria a ação de ?
Passo 1
Vamos primeiramente comparar a função com a equação matricial .
Logo,
Passo 2
Agora, vamos resolver a equação matricial . A matriz é uma matriz tal qual:
Assim:
Passo 3
Agora que obtivemos a função , vamos aplicar os valores e observar o vetor obtido:
Passo 4
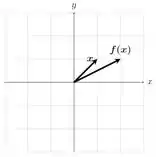
Por último, vamos plotar os vetores e no plano cartesiano.
O vetor terá as coordenadas enquanto o vetor terá coordenadas .
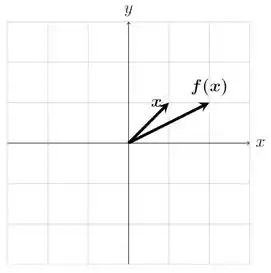
Resposta