Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 8.Problemas Propostos - Ex. 2o
Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa.
Passo 1
O primeiro passo para reduzir uma equação na forma canônica é fazer com que os termos de maior grau fiquem isolados de termos de menor grau.
Sendo a nossa equação :
Isolando:
Tirando a raíz quadrada:
Isso significa que aqui temos a formação de dois planos:
Passo 2
Assim, podemos cruzar os dois planos em um gráfico:
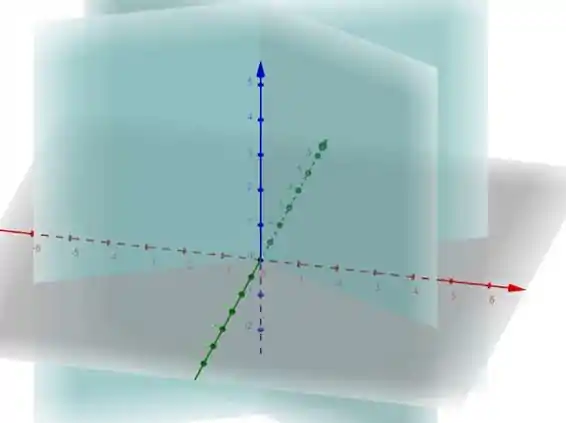
Resposta
Dois planos, .
Exercícios de Livros Relacionados
Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa. 4 x 2 + 2 y 2 + z 2 = 1
Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa. x 2 + 4 y 2 - z 2 = 0
Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa. 4 x 2 - 9 y 2 - 36 z = 0
Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa. y 2 = x 2 + z 2