Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 8.Problemas Propostos - Ex. 2e

Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa.

x 2 + y 2 - 9 z = 0

Passo 1

O primeiro passo para reduzir uma equação na forma canônica é fazer com que os termos de maior grau fiquem isolados de termos de menor grau.

Sendo a nossa equação :

x 2 + y 2 - 9 z = 0

Isolando:

x 2 + y 2 = 9 z

O próximo passo é analisar as fórmulas propostas pelo livro no capítulo 8 e fazer uma comparação superficial , para dizer qual o tipo da nossa equação.

Passo 2

De acordo com o capítulo 8, nós temos aqui a equação de uma Parábola. Se nas equações um dos termos de tiverem sinais iguais, a equação representa um parabolóide circular:

x 2 a 2 + y 2 b 2 = c z

Dessa forma, nossa equação:

x 2 1 + y 2 1 = 9 z

Passo 3

Como c > 0 , a superfície é situada acima do plano x O y , temos uma estrutura que aumenta o tamanho a medida que se afasta do plano. Os traços nos planos x = k e y = k são parábolas. Na equação temos a = b , o parabolóide é de revolução e pode ser gerado pela rotação da parábola.

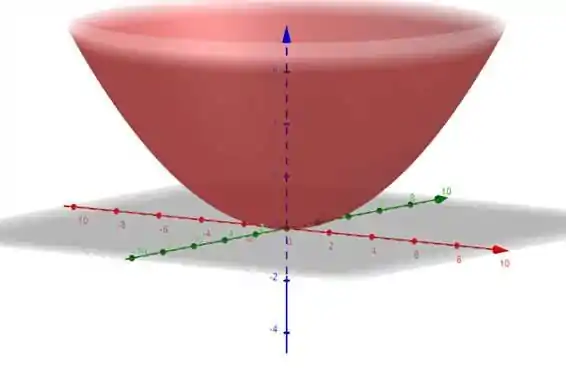
Já para o gráfico em 2D no plano zx temos:

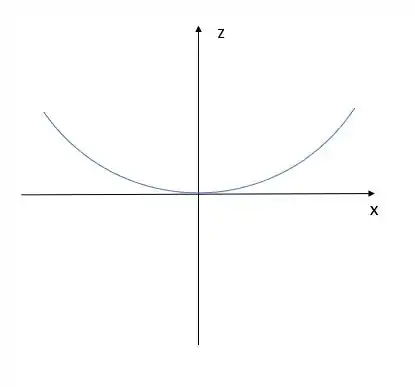
Ufa, agora terminamos!!

Resposta

Parabolóide circular,   x 2 1 + y 2 1 = 9 z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.a) x 2 + y 2 4 = - z 3 , - 3 ≤ z ≤ 0
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.f) y = 6 - x 2 - z 2 , - 3 ≤ z ≤ 6
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.j) z = 4 - 2 x 2 - y 2 , 0 ≤ z ≤ 4
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.i) x = - 4 + y 2 1 + z 2 ,- 4 ≤ x ≤ 5
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. a )25 x 2 + 100 y 2 + 36 z 2 - 900 = 0