Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7a

7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.

a )   25 x 2 + 100 y 2 + 36 z 2 - 900 = 0

Passo 1

L e t r a   a :

Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:

25 x 2 + 100 y 2 + 36 z 2 - 900 = 0

POXA! Eu não sei você está com as mesmas impressões que eu, mas se estiver, vai estar desconfiado de que esta equação nos representa um elipsoide. Vamos ver se é isso mesmo?

Passo 2

Se passarmos esses 900 para o outro lado...

25 x 2 + 100 y 2 + 36 z 2 = 900

E dividir agora todo mundo por 900 ...

25 900 x 2 + 100 900 y 2 + 36 900 z 2 = 1   →

x 2 36 + y 2 9 + z 2 25 = 1   →

Então, colocando todos esses números em forma de quadrado...

x 2 6 2 + y 2 3 2 + z 2 5 2 = 1

AHA! Não falei contigo que essa equação era a equação de um elipsoide?

Passo 3

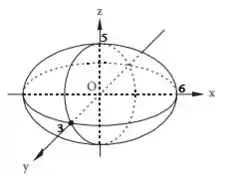
Uma das soluções dessa equação nos darão os pontos ± 6 ,   0 ,   0 , 0 ,   ± 3 ,   0 e 0,0 ,   ± 5 que são os pontos onde o elipsoide corta os eixos. Então repare que o maior eixo do elipsoide é o x , seguido pelo z e por último o y .

Podemos desenhar esse cara (basta desenhar uma bola de basquete com o maior eixo em x ).

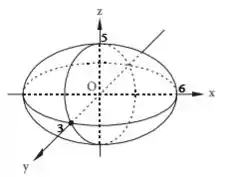
Resposta

Elipsoide:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Descreva a curva interseção do paraboloide Ω com o plano π e determine, quando for o caso, centro, focos, vértices, excentricidade, assíntotas, raio etc. Ω : z + x 2 + 3 y 2 = 0 π : z + 9 = 0 Ω : 4 y
Descreva a curva interseção do paraboloide Ω com o plano π e determine, quando for o caso, centro, focos, vértices, excentricidade, assíntotas, raio etc. Ω : z + x 2 + 3 y 2 = 0 π : z + 9 = 0 Ω : 4 y
Seja Ω a quádrica de equação x 2 + 6 z 2 - 4 x + y - 12 z = 0 . Faça uma translação do sistema de coordenadas para eliminar os termos de primeiro grau e identifique a quádrica.Obtenha, em relação ao s
Prove que, se a ≠ b [respectivamente, a = b ], a quádrica Ω : x + h 2 a 2 + z + l 2 b 2 + y + k = 0 é um paraboloide elíptico [respectivamente, de rotação] de vértice - h , - k , - l e eixo de simetri
Obtenha uma equação do lugar geométrico dos pontos de E 3 que são equidistantes de π : x = 2 e P = - 2,0 , 0 , e identifique-o. Compare com a definição de parábola dada no Capítulo 22.